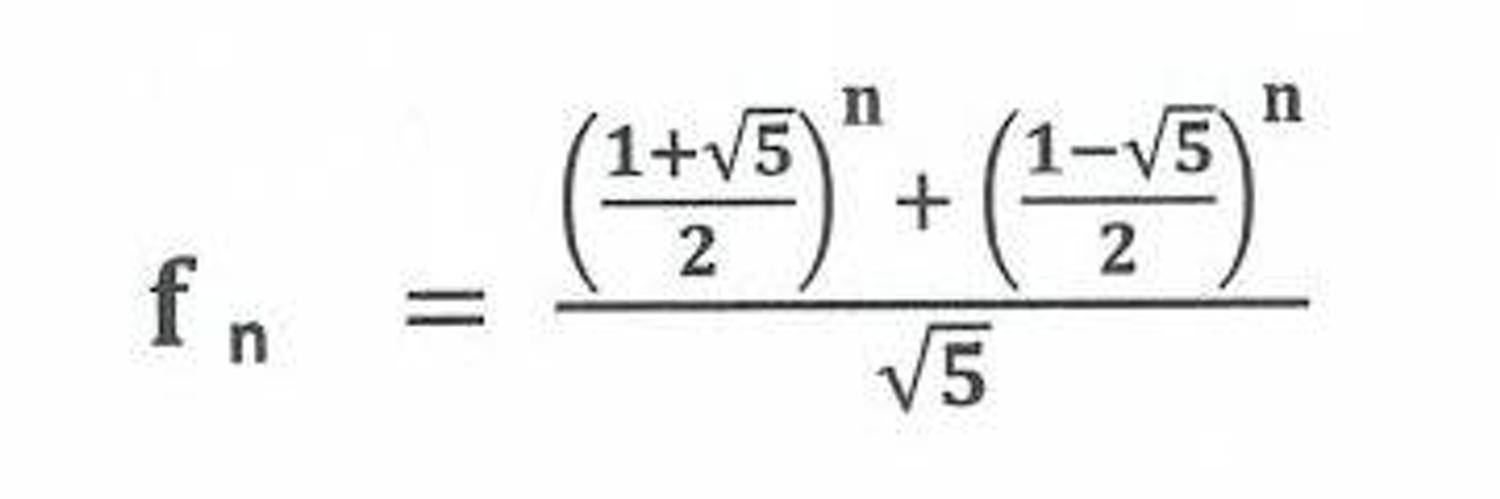Что такое числа Фибоначчи: формула

Доказательство по индукции

Формула F0 +F1 +F2 +…+Fn =Fn+2 –1. представляет собой бесконечно много формул в свернутом виде. Доказать, что F0 +F1 +F2 +…+Fn =Fn+2 –1. верно для конкретного значения n, скажем для n = 6, — простая арифметическая задача. Достаточно будет записать числа от F0 до F6 и сложить их: F0 +F2 +…+F6 =1+1+2+3+5+8+13=33.

Несложно увидеть, что F8 = 34, поэтому формула действует. Перейдем к F7. Не будем тратить время и складывать все числа: мы уже знаем сумму вплоть до F6. Таким образом, (F0 +F1 +…+F6)+F7 =33+21=54. Как и раньше, все сходится: F9 = 55.

Если сейчас мы начнем проверять, работает ли формула для n = 8, наши силы окончательно иссякнут. Но все же посмотрим, что мы уже знаем и что хотим выяснить:

F0 +F1 +…+F7 =F9.

F0 +F1 +…+F7 +F7 =?

Воспользуемся предыдущим результатом: (F0 +F1 +…+F7)+F8 =(F9-1)+F8.

Мы, конечно, можем вычислить (F9-1) + F8 арифметически. Но так мы устанем еще больше. В то же время мы знаем, что F8 + F9 = F10. Таким образом, нам не нужно ничего высчитывать или заглядывать в таблицу чисел Фибоначчи:

(F0 + F1 +… + F7) + F8 = (F9-1) + F8 = (F8 + F9-1) = F10-1.

Мы удостоверились, что формула работает для n = 8, на основе того, что знали про n = 7.

В случае n = 9 мы точно так же опираемся на результат для n = 8 (убедитесь в этом самостоятельно). Разумеется, доказав верность F0 +F1 +F2 +…+Fn =Fn+2 –1. для n, мы можем быть уверены, что F0 +F1 +F2 +…+Fn =Fn+2 –1. верно и для n + 1.

Мы готовы дать полное доказательство. Как уже было сказано, F0 +F1 +F2 +…+Fn =Fn+2 –1. представляет собой бесконечное количество формул для всех значений n от нуля до бесконечности. Посмотрим, как работает доказательство.

Вначале мы доказываем F0 +F1 +F2 +…+Fn =Fn+2 –1. в простейшем случае, для n = 0. Мы просто проверяем, что F0 = F0+2 — 1. Так как F0 = 1, а F2 = 2, очевидным образом 1 = 2 — 1, а F0 = F2-1.

Дальше нам достаточно показать, что верность формулы для одного значения n (скажем, n = k) автоматически означает верность для n + 1 (в нашем примере n = k + 1). Нам лишь надо продемонстрировать, как устроено это «автоматически». Что нам нужно сделать?

Возьмем некоторое число k. Предположим, мы уже знаем, что F0+F1+…+Fk =Fk+2–1. Мы ищем величину F0 + F1 +… + Fk + Fk+1.

Мы уже знаем сумму чисел Фибоначчи вплоть до Fk, поэтому у нас получается:

(F0+F1+…+Fk)+Fk+1 =(Fk+2–1)+Fk+1.

Правая часть равна Fk+2 — 1 + Fk+1, и мы знаем, чему равна сумма следующих друг за другом чисел Фибоначчи:

Fk+2–1 + Fk+1 = (Fk+2 + Fk+1) — 1 = Fk+3– 1

Подставим в наше равенство:

(F0+F1+…+Fk)+Fk+1 =Fk+3–1

Сейчас я объясню, что мы сделали. Если мы знаем, что F0 +F1 +F2 +…+Fn =Fn+2 –1. верно, когда мы суммируем числа вплоть до Fk, тогда F0 +F1 +F2 +…+Fn =Fn+2 –1. должно быть верно, если мы приплюсуем Fk+1.

Подытожим:

— Формула F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для n = 0.

— Если формула F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для n, она верна и для n + 1.

Мы можем уверенно сказать, что F0 +F1 +F2 +…+Fn =Fn+2 –1. верно для любых значений n. Верно ли F0 +F1 +F2 +…+Fn =Fn+2 –1. для n = 4987? Это так, если выражение верно для n = 4986, что основано на верности выражения для n = 4985, и так далее до n = 0. Следовательно, формула F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для всех возможных значений. Этот метод доказательства известен под названием математическая индукция (или доказательство по индукции). Мы проверяем базовый случай и даем шаблон, по которому каждый следующий случай может быть доказан на основе предыдущего.

Простейшее определение чисел Фибоначчи

В первую очередь теоретическая часть. Числа Фибоначчи простыми словами — это последовательность чисел, где каждое следующее число равно сумме двух предыдущих. Началом последовательности, как правило, выступает единица, но в некоторых версиях и 0.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…

Как видите, ничего особо сложного тут нет:

1 + 1 равняется 2;
1 + 2 равняется 3;
2 + 3 равняется 5 и т.д.

Ещё один важный факт — отношение каждого числа к предыдущему будет стремиться к числу 1,618, более известному, как «Золотое сечение». Например, если мы разделим 55 на 34, то примерно получим 1,617, чем больше числа, тем ближе будет к 1,618.

Для общего понимания этой последовательности не требуется знаний математических формул, достаточно уметь складывать числа на школьном уровне. Теперь вы примерно понимаете, о чём идёт речь. Какое именно отношение числа Фибоначчи имеют к трейдингу, я расскажу в следующих разделах, а пока немного истории.

Как использовать золотое сечение в жизни.

В этой статье речь пойдет об очень важном секрете, о котором знают немногие бизнесмены, и незнание которого часто приводит к развалу бизнеса. Есть такие известные понятия, как “золотое сечение” и “числа Фибоначчи”.Ряд Фибоначчи – это когда сумма двух предыдущих чисел дает следующее число

Т.е. 0,1,1,2,3,5… и т.д. В природе все построено по этому принципу. Например, если подсчитать веточки дерева, можно убедиться, что с увеличением радиуса кроны их число увеличивается по закону золотого сечения.Прямоугольник с отношением сторон 0.618 и 0.382 – золотой прямоугольник. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности.Другой всем знакомый пример – пятиконечная звезда (она же магический символ, пентаграмма), в которой каждая из пяти линий делит другую в точке золотого сечения, а концы звезды являются золотыми треугольниками.Скелет человека также построен по этому закону. Он выдержан в пропорции, близкой к золотому сечению. И чем ближе пропорции к формуле золотого сечения, тем более идеальным выглядит внешность человека. Если расстояние между ступней человека и точкой пупа = 1, то рост человека = 1.618 (разумеется, это в идеале). Число 1.618 и есть коэффициент золотого сечения.Но какое отношение это имеет к бизнесу, деньгам, финансам?! Так вот, самое непосредственное! Закон Фибоначчи и есть та самая формула, по которой добывают богатство во все времена. И все, что вы будете предпринимать в соотношении с числами золотого сечения, будет обречено на успех. И наоборот, игнорирование этого правила приводит к краху. Это своего рода магия денег.Рассмотрим применение закона золотого сечения в бизнесе на практике. Допустим, вы купили ящик апельсинов за 1 доллар (доллар в данном случае условная единица) и продали за 2 доллара. Получили прибыль 100%. Как действовать дальше? Купить на эти 2 доллара еще 2 ящика и продать?НЕТ! Вот это и есть самая распространенная ошибка горе-бизнесменов! Правильно будет, в соответствии с законом золотого сечения, купить еще один ящик, продать с теми же 100% прибыли, и только потом купить 2 ящика. То есть действуем по указанному принципу:0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393,196418,317811, Как видим, всего за 32 цикла мы достигли прибыли свыше миллиона! И при этом у нас еще и всегда оставались “лишние” деньги! Кроме того, этот принцип – хорошая страховка от форс-мажорных обстоятельств. Ведь если в самом начале, получив прибыль в 1 доллар и имея 2 доллара на руках и вложив их все сразу, есть риск потерять все. А так у нас доллар в запасе остался, во всяком случае, не в минус уйдем.Особенно важна эта схема при игре на бирже и прочих сравнительно рискованных финансовых операциях. Пример схематичный, его можно адаптировать к прибыли и в 20%, и к любой другой. Используйте в своих расчетах число 1,618 – коэффициент, по которому следует увеличивать финансы, и вам будет сопутствовать успех!Любую деятельность разумно соотносить с принципом золотого сечения. Это самый надежный и безопасный путь. Главное, определиться с единицей измерения. Это может быть время, этапы в работе и т.д. и т.п. Обогащайтесь также поэтапно, согласуя свои шаги с законами природы.

Золотая пропорция в строении легких человека

Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.

Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.

* Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Искусство пространственных форм

Художник Василий Суриков говорил, что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика. Долгое время художники следовали этому закону интуитивно, но после Леонардо ди сер Пьеро да Винчи (итал да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек может означать: Точка — абстрактный объект в пространстве, не имеющий никаких измеримых характеристик, кроме координат золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге Александр Сергеевич Пушкин в селе Михайловском, отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

История метода

Наверное, многим приходилось слышать о так называемой пропорции «золотого сечения», которая используется во многих сферах: математике, физике, биологии и даже искусстве. Это соотношение равняется числу 1,618 и обозначается как Φ.

Так, в правильной пятиконечной звезде значению Φ равны соотношения длин отрезков:

красного к голубому;
голубого к зеленому;
зеленого к желтому.

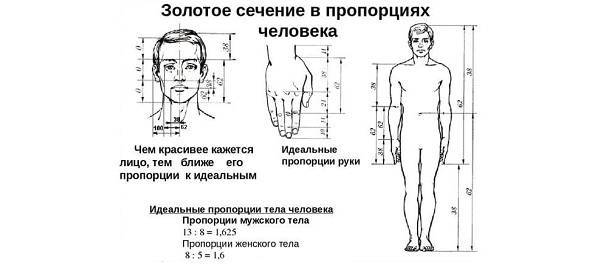
Число Φ выражается формулой:

В XII веке итальянский математик Леонардо Пизано, более известный как Фибоначчи (сын Боначчи), открыл некую закономерность чисел, описанную впоследствии в «Книге Абака». Его отец был моряком и часто путешествовал. Леонардо интересовался математикой и во время путешествий с отцом узнал о числовой последовательности, которая использовалась для стихосложения в древней Индии. Математик углубился в изучение данной закономерности и представил ее европейской науке, в результате чего последовательность получила название чисел Фибоначчи.

Данная последовательность представляет собой числовой ряд:

1-1-2-3-5-8-13-21-34-55-89-144-233-377….. и т.д. до бесконечности.

Особенности последовательности:

Каждое значение равно сумме двух предыдущих. Например, 5+8=13; 34+55=89.
Соотношение предыдущего члена к последующему является результатом, приближенным к значению 0,618: 34/55=0,618; 5/8=0,625. А обратное соотношение дает результат, близкий к числу Φ: 55/34=1,618; 144/89=1,618.
Соотношение значений члена последовательности к следующему через 1 близко к 0,382: 3/8=0,375; 34/89=0,382.
Деление на значение через 2 дает результат, близкий к 0,236: 89/377=0,236; 55/233=0,236.

Где искать золотое сечение?

Математики утверждают, что правило золотого сечения действует и в природе, и в космосе. Наглядный пример красоты и совершенства в природе — это растения и цветы. Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.

Многолетние наблюдения ботаников показали, что растения, чья структура или плоды подчиняются правилам золотого сечения, гораздо более выносливы, а не просто красивы. В одном из исследований по шишкам сибирской сосны или кедра было установлено, что если шишки сильно уклоняются от правильного расположения чешуек, то их семена очень слабо жизнеспособны. Иными словами, только у гармоничной красивой шишки будут жизнеспособные семена.

Числа Фибоначчи можно найти даже у себя. Посмотрите на свои руки: на обеих по пять пальцев. Два из них (большие) состоят из двух фаланг, а у остальных восьми — по три фаланги. 2, 3, 5, 8 — это как раз одни из первых чисел последовательности Фибоначчи. Совпадение? Математики считают, что это закономерно — правило золотого сечения действует повсюду.

Даже в космосе можно найти число идеальной пропорции. Возьмем Солнечную систему. Планеты вращаются по траектории эллипса, а значит, у их траекторий есть минимальный и максимальный радиус. Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.

«Золотая пропорция — это не только критерий красоты, — говорит профессор физического факультета МГУ, доктор физико-математических наук Павел Короленко. — Не только явление, которое позволяет проникнуть в суть понятия красивого. Но это и явление, которое несет в себе некую эвристическую ценность. Задает некое направление в исследованиях, проводимых в математике, физике, биологии

Я считаю, что это очень важное достоинство этого феномена»

Подробнее о золотом сечении и числах Фибоначчи рассказывается в фильме канала «Наука» — «В поисках абсолютной гармонии».

Где встречаются закономерности Фибоначчи?

Вся мистика вокруг Фибо-чисел складывается из того, что они часто встречаются в явлениях природы:

расположение листьев растений;
в семенах подсолнуха;
лепестках цветов;
длина тела в золотом сечении у насекомых (стрекоза);
длина фаланг пальцев у человека и во многом другом.

Нельзя сказать, что числа Фибоначчи — это панацея и ей можно посчитать абсолютно всё, но многие явления так или иначе прослеживаются в такой последовательности чисел, в том числе, это касается психологии человека и трейдинга. На этом я закончу историко-теоретическую часть и перейду непосредственно к финансовым рынкам. Для тех кому, интересна тема, небольшой и очень познавательный ролик о Фибоначчи представлен ниже.

Что думают о последовательности специалисты

Кто-то скажет, что эти числа уже знакомы, потому что они используются в программах технического анализа, для определения величины коррекции и расширения. Кроме того эти же ряды играют важную роль в волновой теории Элиота. Они являются его числовой основой.

Наш эксперт Николай Проверенный портфельный менеджер инвестиционной компании Восток.

– Николай, как вы думаете, случайно ли появление чисел Фибоначчи и его производных на графиках различных инструментов? И можно ли сказать: «Ряд Фибоначчи практическое применение» имеет место?
– К мистике отношусь плохо. А на графиках биржи тем более. У всего есть свои причины. Джо Ди Наполи в книге «Уровни Фибоначчи» красиво рассказывал, где появляется золотое сечение, что не стал удивляться тому, что оно появилось на графиках котировок биржи. А зря! Во многих примерах, которые он привел, часто появляется число Пи. Но его почему-то нет в ценовых соотношениях.
– То есть вы не верите в действенность волнового принципа Элиота?
– Да нет же, не в этом дело. Волновой принцип – это одно. Численное соотношение – это другое. А причины их появления на ценовых графиках – третье
– Каковы на ваш взгляд причины появления золотого сечения на биржевых графиках?
– Правильный ответ на этот вопрос может быть в силах заслужить Нобелевскую премию по экономике. Пока мы можем догадываться об истинных причинах. Они явно не в гармонии природы. Моделей биржевого ценообразования много. Они не объясняют обозначенный феномен. Но не понимание природы явления не должно отрицать явление как таковое.
– А если когда – либо этот закон будет открыт, то сможет ли это разрушить биржевой процесс?
– Как показывает та же теория волн закон изменения биржевых цен – это чистая психология. Мне кажется, знание данного закона ничего не изменит и не сможет разрушить биржу.

Материал предоставлен блогом веб-мастера Максима.

Совпадения основ принципов математики в самых разных теориях кажется невероятным. Может быть это фантастика или подгонка под конечный результат. Поживем – увидим. Многое из того, что раньше считалось необычным или было не возможно: освоение космоса, например, стало привычным и никого не удивляет. Также и волновая теория, может быть непонятная, со временем станет доступней и понятней. То, что раньше было не нужным, в руках аналитика с опытом станет мощным инструментом прогнозирования дальнейшего поведения рынка форекс.

Спираль Архимеда и золотой прямоугольник

Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.

Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.

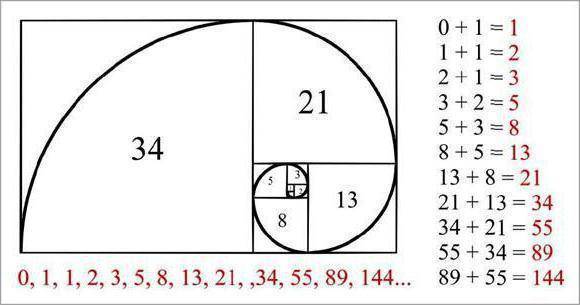
Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» – это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, – спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет

Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

https://youtube.com/watch?v=c3SVIQBXMnA

Золотое сечение в строении микромиров

Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.

В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.

Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.

Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:

Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.

Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.

Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.

В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.

Как рассчитать уровни восстановления Фибоначчи

Последовательность чисел Фибоначчи может использоваться по-разному для получения уровней восстановления Фибоначчи или уровней расширения Фибоначчи . Вот как их найти. Как их использовать, обсуждается в следующем разделе.

Для коррекции Фибоначчи на графике необходимо выбрать две ценовые точки, обычно максимум и минимум колебания . После того, как эти две точки выбраны, числа / линии Фибоначчи рисуются в процентах от этого движения.

Если акция вырастет с 15 до 20 долларов, то уровень 23,6% составит 18,82 доллара, или 20 долларов – (5 долларов x 0,236) = 18,82 доллара. Уровень 50% составляет 17,50 долларов, или 15 долларов – (5 долларов х 0,5) = 17,50 долларов.

Уровни расширения Фибоначчи также выводятся из числовой последовательности. По мере развития последовательности разделите одно число на предыдущее, чтобы получить коэффициент 1,618. Разделите число на два разряда слева, и получится 2,618. Разделите число на три слева, и получится 4,236.

Расширение Фибоначчи требует трех ценовых точек. Начало движения, конец движения, а затем точка где-то посередине (откат).

Если цена вырастет с 30 до 40 долларов, и эти два ценовых уровня являются точками один и два, то уровень 161,8% будет на 16,18 долларов (1,618 x 10 долларов) выше цены, выбранной для точки три. Если третий пункт равен 35 долларам, уровень расширения 161,8% составляет 51,18 доллара (35 долларов + 16,18 доллара).

Уровни 100% и 200% не являются официальными числами Фибоначчи, но они полезны, поскольку проецируют движение, аналогичное (или кратному) тому, что только что произошло на ценовом графике.

Итеративный метод

Можно заметить, что в среде программистов использование рекурсивного метода решения проблемы часто рассматривается как плохая практика, гораздо лучше считаются итеративные методы вычисления. Мы также можем придумать итеративное решение для генерации чисел Фибоначчи:

def iterativeFib(n):    a, b = 0, 1    for i in range(n):        a, b = b, a + b    return a

Этот метод можно использовать для вычисления любого числа Фибоначчи (однако я не проверял его на огромных числах), что также происходит очень быстро, так как всего за 0.0028195 я смог вычислить десятитысячное число Фибоначчи. И если подумать, почему бы не использовать этот метод для вычисления миллионного числа: это возможно, однако займет какое-то время перед тем как полностью загрузиться. Читайте дальше, и я расскажу, почему так происходит.

Что такое числа и линии Фибоначчи?

Числа Фибоначчи используются для создания технических индикаторов с использованием математической последовательности, разработанной итальянским математиком, обычно называемым «Фибоначчи», в 13 веке.Последовательность чисел, начинающаяся с нуля и единицы, создается путем сложения двух предыдущих чисел.Например, ранняя часть последовательности – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т. Д.

Затем эту последовательность можно разбить на коэффициенты, которые, по мнению некоторых, позволяют понять, куда будет двигаться данный финансовый рынок.

Последовательность Фибоначчи важна из-за так называемого золотого сечения 1,618 или его обратной величины 0,618. В последовательности Фибоначчи любое данное число примерно в 1,618 раз больше предыдущего, без учета первых нескольких чисел. Каждое число также составляет 0,618 числа справа от него, опять же без учета первых нескольких чисел в последовательности. Золотое сечение широко распространено в природе, где оно описывает все, от количества жилок на листе до магнитного резонанса спинов в кристаллах ниобата кобальта.

Ключевые выводы

Числа и линии Фибоначчи создаются с помощью соотношений, найденных в последовательности Фибоначчи.
Общие числа Фибоначчи на финансовых рынках: 0,236, 0,382, 0,618, 1,618, 2,618, 4,236. Эти соотношения или проценты можно найти, разделив определенные числа в последовательности на другие числа.
Хотя это официально не числа Фибоначчи, многие трейдеры также используют 0,5, 1,0 и 2,0.
Цифры отражают, как далеко цена может зайти после очередного ценового движения. Например, если акция движется с 1 до 2 долларов, к этому могут быть применены числа Фибоначчи. Падение до 1,76 доллара представляет собой откат на 23,6% от движения цены в 1 доллар (округлено).
Два общих инструмента Фибоначчи – это откаты и расширения. Уровни коррекции Фибоначчи измеряют, насколько далеко может зайти откат. Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна.