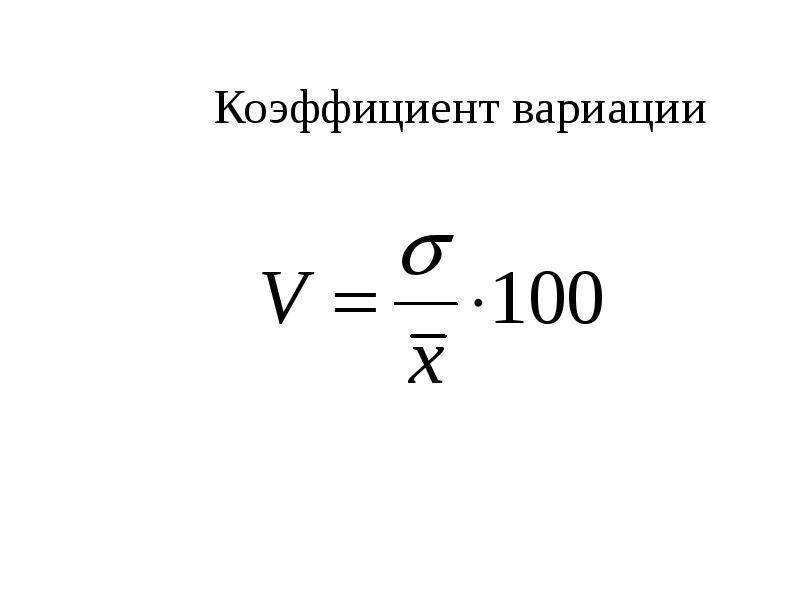Что такое коэффициент вариации и для чего он нужен

Классификация показателей вариации

1. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).
2. Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Показатель	Формула
Средняя арифметическая простая
Средняя арифметическая взвешенная
Средняя гармоническая простая
Средняя гармоническая взвешенная
Мода
Медиана
Размах вариации	R=Xmax-Xmin
Среднее линейное отклонение	;
Дисперсия, Var(x)	;
Среднее квадратическое отклонение
Коэффициент вариации
Коэффициент осцилляции
Линейный коэффициент вариации

Пример использования коэффициента вариации для выбора объекта инвестиций

Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.

Для принятия решения инвестором используется следующая 15-летняя историческая информация:

• SPDR S&P 500 ETF имеет среднюю годовую доходность 5,47% и стандартное отклонение 14,68%. Коэффициент вариации SPDR S&P 500 ETF составляет 2,68;
• Средняя годовая доходность Invesco QQQ ETF составляет 6,88%, а стандартное отклонение-21,31%. Коэффициент вариации QQQ равен 3,09;
• iShares Russell 2000 ETF имеет среднюю годовую доходность 7,16% и стандартное отклонение 19,46%. Коэффициент вариации IWM равен 2,72.

Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.

Вы можете поделиться этой статьёй на своей странице в соцсетях:

Словарь трейдера

olegas ›

Торгую га финансовых рынках с 2008 года. Сначала это был FOREX, затем фондовая биржа. Сначала занимался преимущественно трейдингом (краткосрочными спекуляциями на валютных рынках), но сейчас все больше склоняюсь к долгосрочным инвестициям на фондовом рынке. Хотя иногда, дабы не терять форму и держать себя в тонусе, балуюсь спекуляциями на срочном рынке (фьючерсы, опционы). Пишу статьи на сайт ради удовольствия.

Что предпринимать?

Рекомендовано пройти тщательную диагностику организма. Необходимо выявить причину неправильного уровня. Только после выявления причины или поставленного диагноза следует начинать лечение. Необходимо устранить факторы и причины появления разноразмерных кровяных частиц.

В случае, если диагноз поставлен не был, то изменение объема лейкоцитов указывает на неправильный образ жизни. В этом случае необходимо изменить распорядок дня, увеличить количество часов сна, придерживаться рекомендуемой диеты. Также необходимо отказаться от приема лекарственных средств, увеличить число продуктов, содержащих витамин В12.

Нельзя заниматься самолечением. Это может негативно отразиться на здоровье человека. Необходимое лечение может назначить только лечащий врач.

RDW повышен: связь с заболеваниями

Повышенные значения RDW могут указывать, но не диагностировать и не подтверждать, следующие заболевания: 

• Недостаток железа в организме или авитаминоз
• Недостаток витаминов группы В, включая В12 и фолиевой кислоты
• Анемия (различные типы, включая серповидноклеточную анемию)
• Воспаление
• Бессонница
• Сердечно-сосудистые заболевания
• Кровопотеря из-за кровотечения (включая хирургию)
• Талассемия
• Заболевание печени
• Заболевание почек
• Рак
• Болезнь Альцгеймера
• Алкоголизм
• и другие.

Однако, показатель RDW может все еще находиться на нормальном уровне у людей с лейкемией, или с некоторыми типами анемий (как апластическая анемия). Поэтому важно смотреть не только на значение RDW, но и на взаимосвязь с другими маркерами. 

Среднеквадратичное отклонение — что это

Стандартное (или среднеквадратичное) отклонение – это квадратный корень из дисперсии. В свою очередь, под последним термином подразумевается степень разброса значений. Для получения дисперсии, и, как следствие, ее производного в виде стандартного отклонения, существует специальная формула, которая, впрочем, нам не так важна. Она довольно сложная по своей структуре, но при этом ее можно полностью автоматизировать средствами Excel. Главное – знать, какие параметры нужно передавать функции. В целом как для вычисления дисперсии, так и стандартного отклонения, аргументы используются одинаковые.

1. Сначала мы получаем среднее арифметическое.
2. После этого каждое исходное значение сопоставляется со средним и определяется разница между ними.
3. После этого каждая разница возводится во вторую степень, после чего получившиеся результаты складываются между собой.
4. Наконец, финальный шаг – деление получившегося значения на общее количество элементов в данной выборке.

Получив разницу между одним значением и средним арифметическим всей выборки, мы можем узнать расстояние к нему от определенной точки на координатной прямой. Начинающему человеку вся логика понятна равно до третьего шага. Зачем возводить значение в квадрат? Дело в том, что иногда разница может быть отрицательной, а нам нужно получить положительное число. И, как известно, минус на минус дает плюс. А далее нам нужно определить среднее арифметическое из получившихся значений. Дисперсия имеет несколько свойств:

1. Если выводить дисперсию из одного числа, то она всегда будет равняться нулю.
2. Если случайное число умножить на константу А, то дисперсия увеличится в количество раз, равное А в квадрате. Проще говоря, константу можно вынести за знак дисперсии и возвести его во вторую степень.
3. Если к произвольному числу добавить константу А или же отнять ее, то дисперсия от этого не поменяется.
4. Если два случайных числа, обозначаемых, к примеру переменными X и Y не зависят друг от друга, то в таком случае для них справедлива формула. D(X+Y) = D(X) + D(Y)
5. Если же в предыдущую формулу внести изменения и пытаться определить дисперсию разницы этих значений, то она также будет составлять сумму этих дисперсий.

Среднеквадратическое отклонение – это математический термин, являющийся производным от дисперси. Получить его очень просто: достаточно извлечь квадратный корень из дисперсии.

Разница между дисперсией и стандартным отклонением находится сугубо в плоскости единиц измерения, если можно так выразиться. Стандартное отклонение является значительно более простым для считывания показателем, поскольку оно показывается не в квадратах числа, а непосредственно в значениях. Простыми словами, если в числовой последовательности 1,2,3,4,5 средним арифметическим является 3, то соответственно, стандартным отклонением будет число 1,58. Это говорит о том, что в среднем одно число отклоняется от среднего числа (которым является тройка в нашем примере), на 1,58.

Дисперсия же будет тем же самым числом, только возведенным в квадрат. В нашем примере – чуть меньше, чем 2,5. В принципе, можно использовать как дисперсию, так и стандартное отклонение для статистических расчетов, только надо четко знать, с каким именно показателем пользователь работает.

Расшифровка анализа

Норма RDW составляет 11,5-14,5% для взрослых независимо от возраста, 14,9-18,7% — для детей до полугода, 11,6-14,8% — для детей старше полугода. Если значение меньше или превышает норму, необходимо обследоваться на предмет заболеваний и пройти лечение.

У детей и взрослых RDW бывает повышен при анемиях (железодефицитной, гемолитической, мегалобластной), дефиците витамина B12 и фолатов, заболеваниях печени.

Уровень RDW ниже нормальных показателей может свидетельствовать о развитии анемий разного вида.

При расшифровке анализа учитываются значения MCV. Это помогает при диагностике различать разные виды микроцитарных анемий. Если RDW нормальный, а MCV понижен, это может говорить о таких заболеваниях, как:

• гемотрансфузия;
• талассемия;
• геморрагия;
• посттравматическая спленэктомия;
• злокачественные опухоли и проведенный курс химиотерапии.

Если при пониженном MCV показатель RDW повышен, то это может свидетельствовать о бета-талассемии, дефиците железа, фрагментации эритроцитов. При повышенном MCV и нормальном RDW речь может идти о болезнях печени.

Если оба показателя имеют высокое значение, то есть вероятность дефицита витамина B12, гемолитической анемии, холодовой агглютинации. Кроме того, такой результат наблюдается при прохождении химиотерапии.

Видео о методике забора крови из вены для исследования RDW:

Другие статьи по данной теме:

• назад: Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
• далее: Выборочное наблюдение: понятие, виды, ошибки выборки, оценка
  результатов. Примеры решения задач

Список использованных источников

1. Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями.
   Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
2. Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики,
   информатики, финансов и права. – М., 2003;
3. Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
4. Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика»
   для студентов экономических специальностей: УрГЭУ, 2007;

Для чего нужен коэффициент вариации?

Коэффициент вариации служит для:

– Сравните изменчивость между распределениями, в которых единицы различаются. Например, если вы хотите сравнить вариативность измерения расстояния, пройденного двумя разными транспортными средствами, один из которых был измерен в милях, а другой – в километрах.

– Сравните вариативность между распределениями, в которых единицы равны, но их реализация сильно различается. Пример сравнения вариативности измерения расстояния, пройденного двумя разными транспортными средствами, оба измеряются в километрах, но в котором одно транспортное средство проехало в общей сложности 10 000 км, а другое – только 700 км.

– Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.

– Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.

Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.

Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению

Правило сложения дисперсий

Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).

Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.

Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:

• — групповые средние,
• — численность единиц i-й группы

Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.

— дисперсия i-ой группы.

Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:

на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()

Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:

и показывает насколько вариация признака в совокупности обусловлена фактором группировки.

Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }

оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.

Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:

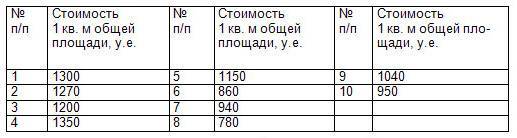
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.

Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле:

.

Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:

а) для домов, построенных вблизи центра:

б) для домов, построенных далеко от центра:

Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:

Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии

Найденные дисперссии в сумме дают величину общей дисперсии

Эмпирический коэффициент детерминации:

показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81,8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18,2% — другими факторами.

Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.

Правило сложения дисперсий для доли признака записывается так:

а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:

общая дисперсия:

Формулы межгрупповой и внутригрупповой дисперсий:

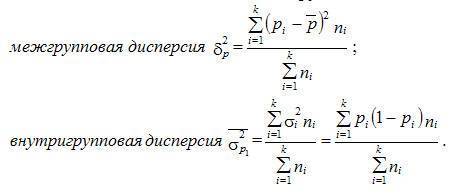
Расчет показателей вариации в Excel

Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel

Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.

Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных.

Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная.

Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.

Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:

— максимальное и минимальное значение

— среднее линейное отклонение

— дисперсия (по генеральной совокупности и по выборке)

— среднее квадратическое отклонение (по генеральной совокупности и по выборке)

— коэффициент вариации

Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом).

Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно.

Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.

Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».

Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.

Среднее линейное отклонение

Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Excel эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.

Среднее квадратическое отклонение

Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.

Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.

Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:

— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г

— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Способы уменьшения RWD

В первую очередь необходимо лечить основное заболевание – причину повышенных значений RDW. Ниже перечислены дополнительные возможности, которые могут помочь вам повысить свой уровень здоровья и снизить показатели RDW.

Сбалансированная диета

Соблюдение здоровой и сбалансированной диеты помогает предотвратить недостаток питательных веществ

Особенно важно, чтобы рацион содержал рекомендованное количество железа, фолиевой кислоты и витамина В12. Исправление дефицита в питании может улучшить производство клеток крови и снизить значения RDW

Снизить потребление алкоголя

Уменьшение потребления алкоголя может помочь снизить повреждение эритроцитов.   Кроме того, алкоголь также снижает поглощение питательных веществ, таких как витамин В12 и фолиевая кислота, которые необходимы для производства красных кровяных клеток.

Больше физической нагрузки

Люди, которые немного или практически не занимаются физической активностью, показывают более высокие уровни RDW.

Физические упражнения, включая упражнения легкой интенсивности, как было показано в исследованиях, улучшают показатели RDW.

В исследовании с участием более чем 8.000 человек, при увеличении количества времени физических тренировок в неделю, риск показать повышенный уровень RDW уменьшался на 11%. 

Бросить курить

Курение увеличивает окислительный стресс. У курильщиков определяется более высокие RDW и они связаны с количеством выкуриваемых сигарет в день, а также с продолжительностью курения. 

Достаточный сон

В исследовании с  участием 17.500 взрослых людей, те, кто спал 7-8 часов, показывали самые низкие значения RDW. Люди, которые спали менее 6 часов, около 10 часов и более 10 часов демонстрировали увеличение RDW на 23%, 29% и 67% соответственно. 

Оцените эту статью

Среднее 4.8 Всего голосов (5)

среднее квадратическое отклонение

Или стандартное отклонение. Оно обозначается греческой буквой «сигма», и коль скоро, у нас выборочная совокупность, то добавляем соответствующий подстрочный индекс:

 – выборочное среднее квадратическое отклонение.

Чем меньше стандартное отклонение (и дисперсия), тем меньше вариация – тем бОльшее количество вариант находится вблизи выборочной средней. Но у нас, как нетрудно «прикинуть на глазок», разброс довольно-таки велик – значительное количество вкладов расположено далековато от , и поэтому значение  получилось немалым.

Следующая часть задачи состоит в том, чтобы корректно оценить генеральную дисперсию  и генеральное среднее квадратическое отклонение .

В 1-й части урока я рассказал о том, что выборочная дисперсия  представляет собой смещённую оценку генеральной дисперсии. Это означает, что если мы будем проводить неоднократные выборки из той же генеральной совокупности, то полученные значения  будут систематически занижено оценивать

Обращаю ваше внимание, что это не значит, что  будет всегда меньше, чем

И поэтому выборочную дисперсию, как намекает условие, нужно поправить: – исправленная выборочная дисперсия

и, соответственно: или 240,30 д.е. – исправленное среднее квадратическое отклонение.

 и  – это уже несмещённые оценки генеральной дисперсии  и генерального стандартного отклонения  соответственно.

Ввиду большого объёма выборки (более 100 вариант) этой поправкой можно пренебречь, но всё же мы не будем «разбрасываться» 30 «копейками».

Ответ: ; в качестве оценки соответствующих генеральных показателей принимаем  и .

Рассмотренные выше показатели (размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение) входят в группу абсолютных показателей вариации, которые обладают рядом неудобств. Так, если в прорешанной задаче не уменьшать варианты в 1000 раз, то дисперсия получится в миллион раз больше! Да-да, не , а . И возникает естественное желание привести результаты к некому единому стандарту.

Для этого существуют показатели относительные, и самым известным из них является

Что такое RDW?

Эритроциты – это красные тельца двояковогнутой дисковидной формы, окрашивающие кровь в соответствующий цвет. Они составляют основу крови и снабжают кислородом ткани и органы. У здоровых людей они не отличаются по объему, цвету и форме. Правильная работа красных кровяных клеток зависит не от их диаметра, а именно от объема. Его средний показатель обозначается MCV. У здоровых людей это значение может колебаться в незначительных пределах. В медицине этот диапазон называют гетерогенностью эритроцитов, или шириной распределения по объему. Обычно красные клетки уменьшается в объеме с возрастом человека, таким образом, между ними появляется разница. Кроме того, это может быть связано с анемией или злокачественными опухолями. Появление в крови эритроцитов, разных по объему, называется анизоцитозом. Для того чтобы установить изменения, врач направляет сдать кровь на RDW.

RDW повышен

Высокий RDW означает, что ваши красные кровяные клетки (эритроциты) неравны по размеру. Такое состояние называется анизоцитозом.  Это происходит, когда по какой-либо причине у вас возникают проблемы с образованием эритроцитов.

Анизоцитоз определяется показателем RDW и классифицируется согласно размерам эритроцитов вместе с MCV (средним объемом эритроцита):

• Анизоцитоз с микроцитозом (малыми размерами эритроцитов). Возможные причины: дефицит железа, серповидноклеточная анемия.
• Анизоцитоз с макроцитозом (большие размеры эритроцитов). Возможные причины: дефицит витамина В12 или фолиевой кислоты, аутоиммунная гемолитическая анемия, проведение цитотоксической химиотерапии, хроническое заболевание печени,  миелодиспластический синдром.
• Анизоцитоз с нормальными размерами эритроцитов. Возможные причины: дефицит железа, недостаток витамина В12 или фолиевой кислоты, диморфная анемия, серповидноклеточная анемия, хроническая болезнь печени, миелодиспластический синдром.

АНОМАЛЬНЫЕ ФОРМЫ И РАЗМЕРЫ ЭРИТРОЦИТОВ

Что такое RDW

Ширина распределения красных кровяных клеток (RDW) – это изменение размера (объема) эритроцитов – красных кровяных клеток. В принципе, этот тест говорит вам, насколько равны или неравны ваши красные кровяные клетки в размере. Показатель RDW это часть полного анализа крови, который также измеряет показатели гемоглобина, гематокрита, а также количество красных и белых кровяных клеток. 

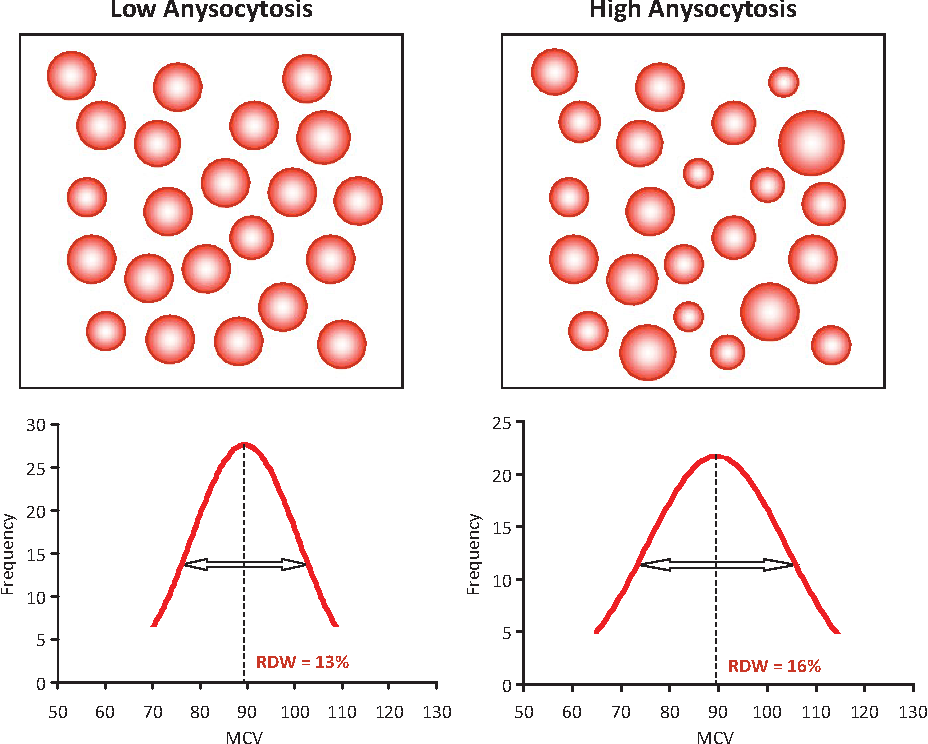СЛЕВА – ПОЧТИ ОДИНАКОВЫЕ РАЗМЕРЫ ЭРИТРОЦИТОВ (RDW – В НОРМЕ), СПРАВА – РАЗМЕРЫ ЭРИТРОЦИТОВ СИЛЬНО РАЗНЯТСЯ (RDW -НЕ В НОРМЕ)

Низкие значения RDW означают, что ваши красные кровяные клетки примерно одинаковы по размеру, и такое их состояние нормально и желательно. А вот более высокие значения RDW означают, что ваши красные кровяные клетки производятся в разных размерах. Другими словами, есть некоторые проблемы с производством и выживаемостью эритроцитов.

Величина RDW является важной, но не специфичной (не указывающей на конкретное заболевание) величиной, поэтому ширину распределения эритроцитов по объему используют в комплексе, вместе с другими показателями крови. Поэтому вместе с RDW в анализах крови измеряются и такие показатели, как: MCV (средний объем эритроцита), МСНС (средняя концентрация гемоглобина в эритроците)

Поэтому вместе с RDW в анализах крови измеряются и такие показатели, как: MCV (средний объем эритроцита), МСНС (средняя концентрация гемоглобина в эритроците).

Принципы определения показателей вариации

Пример №4

Средние величины и показатели вариации имеют в статистике важное значение. Они широко применяются для характеристики статистических совокупностей по варьирующим признакам.
В задачах контрольных работ могут приводиться так называемые открытые интервалы, то есть, интервалы, у которых верхняя или нижняя границы точно не определены, а сама граница остается как бы открытой

В этом случае за величину открытого интервала условно принимается величина смежного закрытого интервала. Например, дан вариационный ряд распределения работников магазина:

Группы работающих по величине заработка (руб. в месяц)	Число работающих (чел.)
до 8000	6
от 8000 до 9000	10
от 9000 до 10000	14
и т.д.

определении среднего квадратического отклонения_ix

Пример 2

В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?

Он начинается с вычисления среднего арифметического и стандартного отклонения:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.

Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:

Рассчитываются среднее арифметическое и стандартное отклонение:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.

Замечено, что среднее значение, стандартное отклонение и коэффициент вариации различаются, когда температура измеряется в градусах Цельсия или в градусах Фаренгейта, даже если это одни и те же дети

Шкала интервальных измерений – это та шкала, которая производит эти различия, и поэтому необходимо соблюдать осторожность при использовании коэффициента вариации для сравнения переменных на разных шкалах

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение  хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей 🙂

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке 🙂

Задание 8

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Решения и ответы:

Пример 17. Решение:

а) Используем формулу . По условию, , . Таким образом: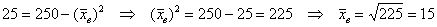

б) Используем формулу . По условию, , . Таким образом:

Ответ: а) , б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле: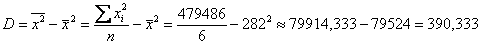Среднее квадратическое отклонение: тонн.Коэффициент вариации:

Ответ:  тонны,  тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил  тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

(Переход на главную страницу)