Нулевая гипотеза в статистике: пример. Проверка нулевой гипотезы

Что это и кому это нужно?

Проверка (тест) статистической гипотезы – это способ математического определения верности некоторого утверждения на основе
закона распределения. Освоив этот метод, Вы сможете делать математически обоснованные выводы, например:

Пример #1

Вы изготавливаете кубики для игры в кости и чтобы убедиться, что кубик отлично сбалансирован, Вы проводите тест – бросаете кости 600 раз
и решаете, что если каждое число выпало 100±10 раз, то кубик сбалансирован.

Пример #2

На производстве 5% продукции отбраковывается, Вы разработали новую технологию и хотите проверить, уменьшится ли
количество брака.

Критерии проверки статистических гипотез

Понятие статистической гипотезы

 Статистической гипотезой (гипотезой) называется любое утверждение об изучаемом законе распределения или характеристиках случайных величин.

Пример статистических гипотез:

1. Генеральная совокупность распределена по нормальному закону.
2. Дисперсии двух нормально распределенных совокупностей равны между собой.

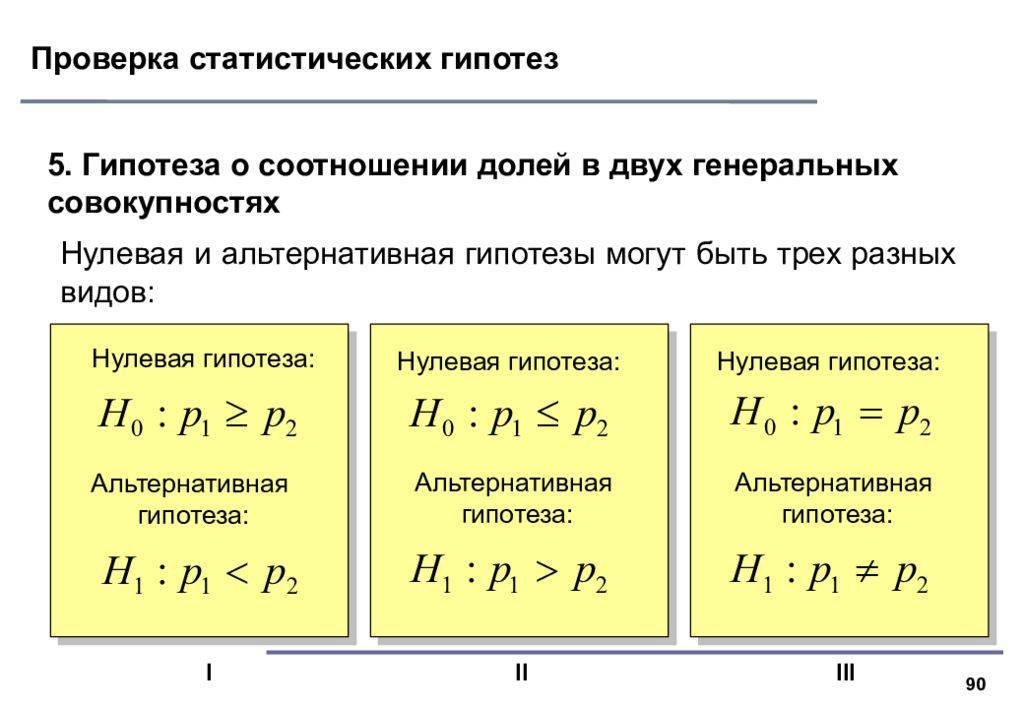
Нулевая гипотеза (Н) — предположение о том, что между  параметрами генеральных совокупностей нет различий, то есть эти различия носят не систематический, а случайный характер.

Пример1. Нулевая гипотеза записывается следующим образом:

H: µ₁=µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности равно генеральному среднему другой совокупности).

 Альтернативная гипотеза (Н₁) – предположение о том, что между параметрами генеральных совокупностей есть достоверные различия.

 Пример 2. Альтернативные гипотезы записываются следующим образом:

• H₁: µ_1≠µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности не равно генеральному среднему другой совокупности).
• H₁: µ₁>µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности больше генерального среднего другой совокупности).
• H₁: µ_1<µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности меньше генерального среднего другой совокупности).

Ошибки при проверке гипотез

Ошибки, допускаемые при проверке статистических гипотез, делятся на два типа:

• ошибки первого рода;
• ошибки второго рода.

Ошибка первого рода – отклонение гипотезы Н, когда она верна. Вероятность ошибки первого рода обозначается α и называется уровнем значимости.

Ошибка второго рода – принятие гипотезы Н, когда верна альтернативная гипотеза. Вероятность ошибки второго рода обозначается β.

Более подробно о методах статистической обработки данных рассказано в книгах:

• Факторный анализ в педагогических исследованиях в области физической культуры и спорта
• Компьютерная обработка данных экспериментальных исследований
• Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта

Классификация критериев значимости (критериев проверки статистических гипотез)

Для проверки правдоподобия статистической гипотезы используют критерий значимости – метод проверки статистической гипотезы.

Необходимо отметить, что до получения исследователем экспериментальных данных необходимо сформулировать статистическую гипотезу и задать уровень значимости α. При выборе уровня значимости исследователь должен исходить из практических соображений, отвечая на вопрос: какую вероятность ошибки он считает допустимой. В области физической культуры и спорта чаще всего задают уровень значимости α=0,05.

Критерии проверки статистических гипотез (критерии значимости) можно разделить на три большие группы:

1. Критерии согласия;
2. Параметрические критерии;
3. Непараметрические критерии.

 Критерии согласия называются критерии значимости, применяемые для проверки гипотезы о законе распределения генеральной совокупности, из которой взята выборка. Для проверки статистической гипотезы чаще всего используются следующие критерии согласия: критерий Шапиро-Уилки, критерий хи-квадрат, критерий Колмогорова-Смирнова.

Параметрические критерии – критерии значимости, которые служат для проверки гипотез о параметрах распределений (чаще всего нормального). Такими критериями являются: t-критерий Стьюдента (независимые выборки), t-критерий Стьюдента (связанные выборки), F-критерий Фишера (независимые выборки).

Непараметрические критерии – критерии значимости, которые для проверки статистических гипотез не использует предположений о распределении генеральной совокупности. В качестве примера таких критериев можно назвать критерий Манна-Уитни и критерий Вилкоксона.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
3. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Проверка гипотезы об однородности выборок

Существует два вида гипотез об однородности выборок. Может быть
проверена однородность выборок “в слабом”: выборки однородны “в слабом”, если незначимо отличаются их
параметры, прежде всего, среднее. Может быть проверена однородность выборок “в сильном”: выборки
однородны “в сильном”, если незначимо отличаются их законы распределения.

С помощью критерия Стьюдента проверяется гипотеза об однородности выборок “в слабом”.
В этом случае основная гипотеза формулируется следующим образом: математическое ожидание первой
выборки незначимо отличается от математического ожидания второй выборки. Формально это записывается так:
.

Критерий рассчитывается по формуле:

где и
– математические ожидания первой и
второй выборок размерами и
соответственно (в качестве оценок
математических ожиданий берутся значения средних первой и второй выборок);

и
– дисперсии первой
и второй выборок;

–
число степеней свободы.

Критерий может принимать значения от минус бесконечности до плюс бесконечности. Чем
ближе значения критерия к нулю, тем больше вероятность, что основная гипотеза будет верной (при этом знак
не имеет значения).

Пусть задано значение уровня значимости
. Тогда критерий будет принимать значения в области принятия гипотезы с
вероятностью (эта вероятность называется уровнем доверия). Вероятность того,
что критерий примет значения меньшие, чем значение левой критической точки области
принятия гипотезы равна , а вероятность того, что критерий примет значение,
меньшее, чем значение правой критической точки . Значением левой критической
точки области принятия гипотезы будет являться квантиль распределения Стьюдента
уровня с df степенями свободы. Значением правой критической точки области принятия
гипотезы будет выступать квантиль распределения Стьюдента уровня с тем же
числом степеней свободы.

При проверке гипотезы об однородности выборок с помощью критерия Стьюдента
необходимо помнить, что к выборкам выдвигаются допущение, нарушение которых не
позволяет применить критерий:

• выборки должны подчиняться нормальному распределению. Если это требование
  нарушается, то критерий не будет подчиняться распределению Стьюдента и,
  следовательно, границы области принятия гипотезы будут найдены неверно;
• в выборках не должны присутствовать резко выделяющиеся наблюдения, иначе
  среднее значение будет смещено в сторону выбросов и в результате критерий даст
  некорректный результат.

Пример 6. Имеются данные некоторой выборки. По ним в пакете
программных средств STATISTICA вычислены следующие показатели:

Среднее 1-й выборки	Среднее 2-й выборки	t-критерий	Число степеней свободы	p-level
19,60	28,21	-1,38	48	0,17

Область принятия гипотезы при уровне значимости :

Сделать вывод об однородности выборок.

Ответ.

Значение t-критерия попадает в область принятия гипотезы. Может быть принята
основная гипотеза о том, что математическое ожидание первой выборки незначимо отличается от математического ожидания второй выборки. Таким образом, проверена гипотеза об однородности выборок в слабом.

С помощью критерия Колмогорова-Смирнова проверяется гипотеза об однородности выборок
“в сильном”, то есть о том, что функции распределения выборок незначимо отличаются друг от друга. За
основу критерия Колмогорова-Смирнова выступает статистика

–

максимальная по модулю разность между двумя функциями распределения выборок x и y.

Критерий рассчитывается по формуле

Границы области принятия гипотезы определяются следующим образом:

.

Если критерий принадлежит области принятия гипотезы, то при заданном уровне значимости
α нет возможности её отвергнуть, следовательно, принимается гипотеза о том, что выборки
однородны “в сильном”.

Гипотезы об однородности выборок могут быть выдвинуты как в
исследованиях поведения человека,
так и технических науках.

Пример 7. По данным некоторой выборки получены следующие показатели:

Макс. отриц. разность	Макс. полож. разность	Значение критерия K.S.	p-level
-0,2	0,08	0,117	>10

Область принятия гипотезы при уровне значимости :

Сделать вывод об однородности выборок.

Ответ.

Значение критерия попадает в область принятия гипотезы. Следовательно, принимается
основная гипотеза о том, что функции распределения двух выборок незначимо отличаются. Таким образом,
выборки однородны “в сильном”.

Назад

Листать

Вперёд>>>

Всё по теме “Математическая статистика”

Метод проверки гипотез

В реальности истинная средняя по генеральной совокупности неизвестна и ее значение можно только предполагать. Такое предположение называется статистической гипотезой, обозначается H. Если предположение противоречит наблюдаемым данным, то гипотезу отклоняют, как ложную; если не противоречит, то не отклоняют. Степень противоречия определяется вероятностью, которая в свою очередь зависит от того, как далеко фактическая выборочная средняя отклоняется от гипотезы. Если она (вероятность) достаточно маленькая, то противоречие считается доказанным (не забывая о возможной ошибке). Для расчета вероятности выбирают вероятностно-статистическую модель, которая описывает поведение оценки при многократном повторении эксперимента. В случае со средней арифметической в большой выборке подойдет стандартное нормальное распределение.

Теперь нужно определить, какова вероятность извлечь из такой генеральной совокупности имеющуюся выборочную среднюю. Если она окажется в зоне близкой к центру, то это не противоречит гипотезе, ведь такое вполне может произойти в силу случайности. Но если она окажется далеко, например, выйдет за пределы ± 1,96 стандартные ошибки, то это будет означать что, либо произошло маловероятное событие, либо выдвинутая гипотеза ложна и ее следует отклонить.

Правила проверки гипотезы (статистического вывода) показаны на рисунке.

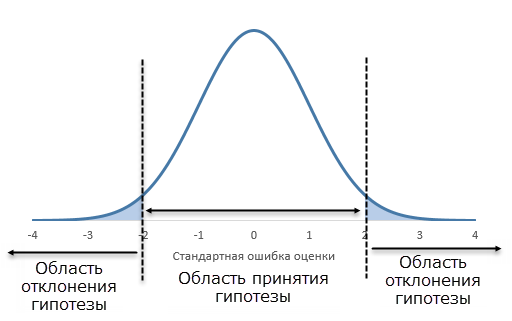
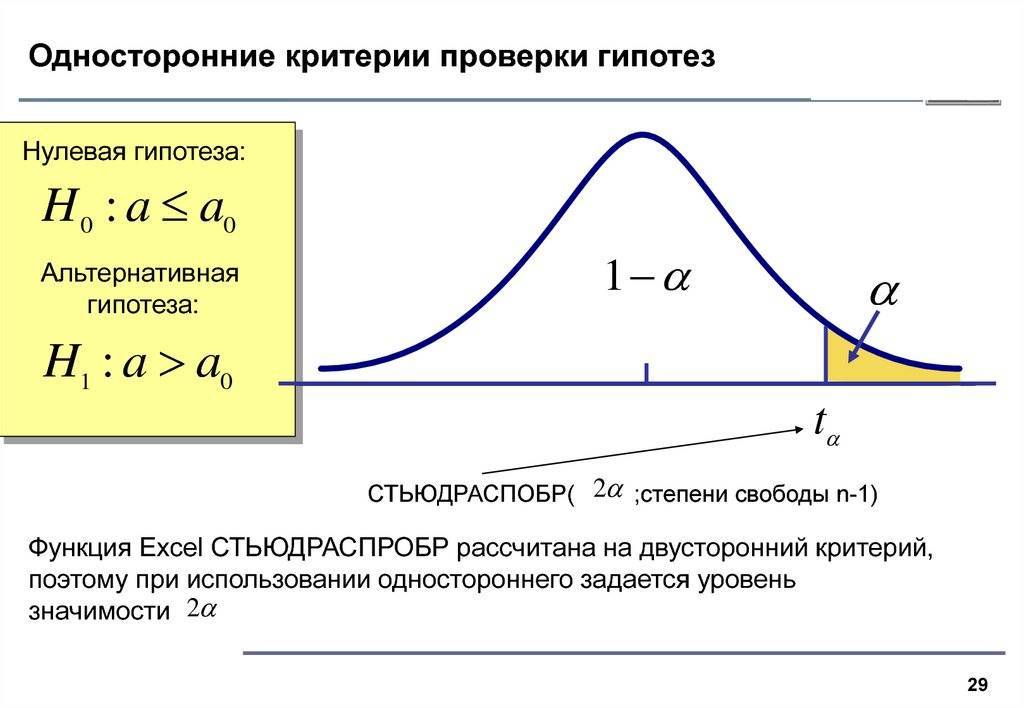
Предельное значение, которое разделяет области принятия и отклонения гипотезы, называется критическим уровнем. Область отклонения гипотезы – критическая область. Вероятность, соответствующая критической области, – уровень значимости, обозначается греческой буквой α (альфа). Например, α = 0,05 означает, что уровень значимости равен 5%. Очевидно, что между критическим уровнем и уровнем значимости существует функциональная взаимосвязь.

Чтобы определить, в какую область попадает выборочная средняя, нужно рассчитать т.н. статистический критерий, иногда говорят статистика. Большие значения критерия, как правило, свидетельствуют в пользу того, что отличие не случайно и, соответственно, гипотеза не верна. Статистический критерий для нормальной модели – это обычная z-оценка, рассчитываемая по известной формуле.

гдеz – критерийx̄ – наблюдаемое среднее арифметическоеμ – гипотетическая средняя в генеральной совокупностиs – среднеквадратическое отклонение выборочных данныхn – объем выборки

Если рассчитанный критерий оказывается по модулю больше, чем критическое значение, т.е. попадает в критическую область, значит, гипотеза отклоняется как ложная (точнее, маловероятная).

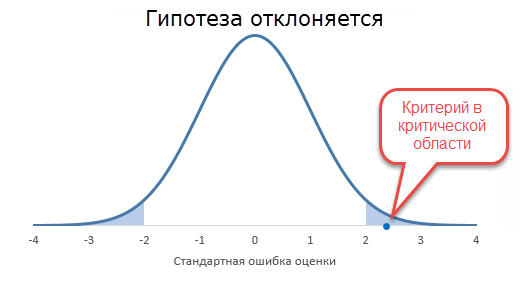
Если критерий не выходит за критическое значение, то гипотеза не отклоняется.

Уровень значимости задается исходя из практических соображений. Часто берут 0,05, для которого критический уровень равен 1,96 (в нормальной модели). Если α = 0,01, то критический уровень – 2,58. Все это легко получить из таблиц стандартного нормального распределения. Но, конечно, быстрее посчитать на компьютере, хоть и в Excel.

В зависимости от выбранной вероятностно-статистической модели вид распределения и способ расчета критерия производится по-разному. Но суть остается прежней: статистический критерий сравнивается с критическим значением, который задается исходя из желаемого уровня значимости.

Принцип

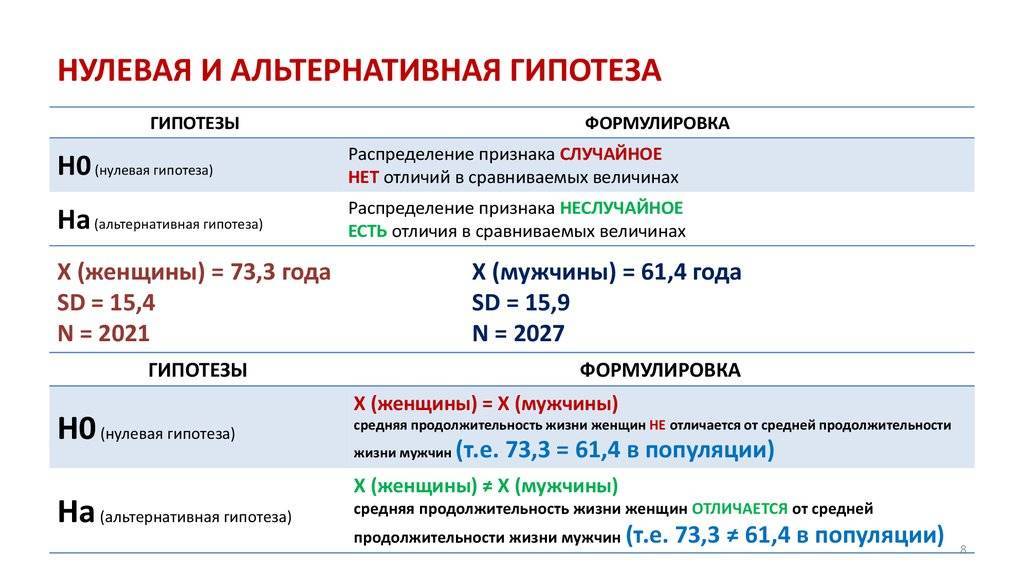
Проверка гипотез требует построения статистической модели того, как бы выглядели данные, если бы за результаты отвечали только случайные или случайные процессы. Гипотеза о том, что за результаты отвечает только случай, называется нулевой гипотезой . Модель результата случайного процесса называется распределением при нулевой гипотезе . Полученные результаты сравниваются с распределением при нулевой гипотезе и тем самым определяется вероятность нахождения полученных результатов.

Проверка гипотез работает путем сбора данных и измерения вероятности конкретного набора данных (при условии, что нулевая гипотеза верна), когда исследование проводится на случайно выбранной репрезентативной выборке. Нулевая гипотеза предполагает отсутствие связи между переменными в генеральной совокупности, из которой выбрана выборка .

Если набор данных случайно выбранной репрезентативной выборки очень маловероятен относительно нулевой гипотезы (определяемой как часть класса наборов данных, которые будут наблюдаться лишь изредка), экспериментатор отвергает нулевую гипотезу, заключая ее (возможно, ) ложно. Этот класс наборов данных обычно определяется с помощью тестовой статистики , которая предназначена для измерения степени очевидного отклонения от нулевой гипотезы. Процедура работает путем оценки того, превышает ли наблюдаемое отклонение, измеренное статистикой теста, заданное значение, так что вероятность появления более экстремального значения мала при нулевой гипотезе (обычно менее 5% или 1%). % аналогичных наборов данных, в которых нулевая гипотеза верна).

Если данные не противоречат нулевой гипотезе, то можно сделать лишь слабый вывод: а именно, что наблюдаемый набор данных не дает достаточных доказательств против нулевой гипотезы. В этом случае, поскольку нулевая гипотеза может быть истинной или ложной, в некоторых контекстах это интерпретируется как означающее, что данные не дают достаточных доказательств для того, чтобы сделать какой-либо вывод, в то время как в других контекстах это интерпретируется как означающее, что нет достаточных доказательств для поддержка перехода с текущего полезного режима на другой. Тем не менее, если на этом этапе эффект кажется вероятным и / или достаточно большим, может появиться стимул к дальнейшим исследованиям, например, к увеличению выборки.

Например, определенный препарат может снизить вероятность сердечного приступа. Возможные нулевые гипотезы: «этот препарат не снижает вероятность сердечного приступа» или «этот препарат не влияет на вероятность сердечного приступа». Проверка гипотезы заключается во введении препарата половине людей в исследуемой группе в качестве контролируемого эксперимента . Если данные показывают статистически значимое изменение среди людей, принимающих препарат, нулевая гипотеза отклоняется.

Гипотеза о равенстве генеральных дисперсий двух нормальных распределений

Две средние мы , очередь за дисперсиями. Из двух нормальных ген. совокупностей извлечены независимые выборки объёмом  и  и найдены их исправленные дисперсии:  и  соответственно. Совершенно понятно, что эти значения случайны и отличны друг от друга. Но возникает вопрос: значимо или незначимо это отличие? Для ответа на этот вопрос на уровне значимости  проверяется гипотеза о равенстве генеральных дисперсий . Если она будет принята, то различие между выборочными значениями   объяснимо случайными факторами.

Для проверки этой гипотезы используют критерий , где  – бОльшая исправленная дисперсия, а  – мЕньшая.

Данная случайная величина имеет (так называемое F-распределение) со степенями свободы , если  или , если . То есть, степень свободы  соответствует выборке с бОльшей исправленной дисперсией.

В качестве альтернативы рассматривают одну из следующих гипотез:

1)  (если ) либо  (если ). Для этой гипотезы строят правостороннюю критическую область:
Критическое значение  можно найти по таблице критических значений F-распределения, а ещё лучше – с помощью стандартной функции Экселя, используйте тот же Калькулятор (Пункт 12).

2)  – для этой гипотезы строится двусторонняя критическая область:
Однако для решения нашей задачи достаточно найти лишь правое критическое значение .

Дело в том, что , и поэтому случайное значение  (бОльшее единицы) заведомо не может попасть в левый кусок критической области.

Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия , и если оно попадает в критическую область ( для обоих случаев), то гипотеза  отвергается. Если , то принимается.

Рассматриваемая гипотеза часто возникает, когда требуется сравнить точность двух приборов, инструментов, станков, двух методов исследования. И сейчас мы разберём эту стандартную задачу:

Пример 47

Некоторая физическая величина измерена  и  раз двумя различными способами. По результатам измерений найдены соответствующие погрешности . Требуется на уровне значимости 0,05 проверить, одинаковую ли точность обеспечивают эти способы измерений.

Ситуации тут могут быть разные: это измерение двумя однотипными инструментами (например, двумя линейками), или инструментами разными (например, линейкой и штангенциркулем), или речь вообще идёт о двух методах измерения (например, с зажмуренным левым и правым глазом).

И возникает вопрос: различие между  случайно или обусловлено тем, что какой-то способ точнее?

Решение: полагая, что погрешности измерений распределены нормально, проверим гипотезу   о том, что точность двух способов одинакова против конкурирующей гипотезы   (она правдоподобнее, нежели ).

Для проверки гипотезы используем критерий , где  – бОльшая исправленная дисперсия, а  – мЕньшая.

Найдём критическое значение . Степень свободы  должна соответствовать выборке с бОльшей дисперсией, следовательно,  и . По соответствующей таблице либо с помощью Калькулятора (Пункт 12) находим:

При  нулевая гипотеза принимается, а при   (в критической области) – отвергается.

Вычислим наблюдаемое значение критерия:, поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу   . Иными словами, различие выборочных значений  обусловлено случайными факторами, но прежде всего, малым количеством опытов.

Так, если бы было проведено в 10 раз больше измерений  и получены те же самые погрешности, то , и гипотеза о равенстве ген. дисперсий уже отвергается. То есть здесь расхождение между  уже нельзя объяснить случайностью, а объяснимо оно именно тем, что второй способ менее точный (справедлива гипотеза ).

Ответ: на уровне значимости 0,05 точность способов измерения одинакова.

Творческая задача для самостоятельного решения, случай из жизни:

Пример 48

Две группы студентов-первокурсников написали контрольную по математическому анализу со следующими результатами: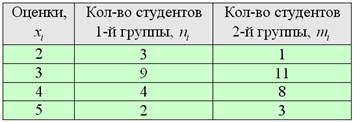
Предполагая, что успеваемость студентов распределена нормально, на уровне значимости 0,1:

1) Проверить гипотезу  – о том, что группы однородны по составу (в плане соотношения лучше и хуже успевающих студентов) против конкурирующей гипотезы ,

и в случае однородности групп :

2) Проверить гипотезу   – об одинаковой успеваемости групп против гипотезы о том, что одна из групп более слабая.

Вспоминаем, что такое дискретный вариационный ряд и как рассчитываются его характеристики. Не позволяй душе лениться! – в жизни пригодится, все числа уже в Экселе.

Ну что, порешаем ещё задачки? …конечно, порешаем! – ведь я маньяк в лучшем смысле этого слова:

P-value

Изложенная выше методика на сегодняшний день несколько устарела. Дело в том, что, сравнивая критерий с критическим уровнем, мы не видим «силу доказательства». Ведь критерий может попасть в область, соответствующую 5% уровню значимости, а может и в 1% значимости (т.е. отклониться еще дальше). В обоих случаях гипотеза отклоняется, но уверенность, с которой это делается, не одинаковая. Одно дело «скорее всего» (как при 5%-м уровне), а другое «наверняка» (как при 1% уровне). Поэтому проверку гипотезы делают по наблюдаемому уровню значимости, который называют p-value (или р-значение).

p-value – вероятность получить наблюдаемое или еще большее отклонение оценки от гипотезы, если она (гипотеза) верна. Геометрически это площадь под кривой, которая начинается от статистического критерия в сторону от гипотезы (от центра).

Общий p-value на данном рисунке складывается из двух частей, т.к. гипотеза рассматривает отклонение в любую из сторон.

Например, если статистический критерий равен 1,96, то вероятность получить по модулю такое или еще большее значение, равна 0,05. Это и есть p-value, который в данном случае совпал с уровнем значимости. Но если критерий равен 3, то вероятность получить такое или еще больше отклонение (по модулю) равна всего 0,0027. Т.к. мы считаем возможным отклонение в обе стороны, p-value складывается из двух частей.

Итак, правило проверки гипотезы по наблюдаемому уровню значимости следующее: если p-value меньше, чем заданный уровень значимости (например, 0,05), то гипотеза отклоняется. В противном случае не отклоняется (не отвергается). В примере выше p-value = 0,0027, что гораздо меньше, чем 0,05. Следовательно, гипотеза отвергается.

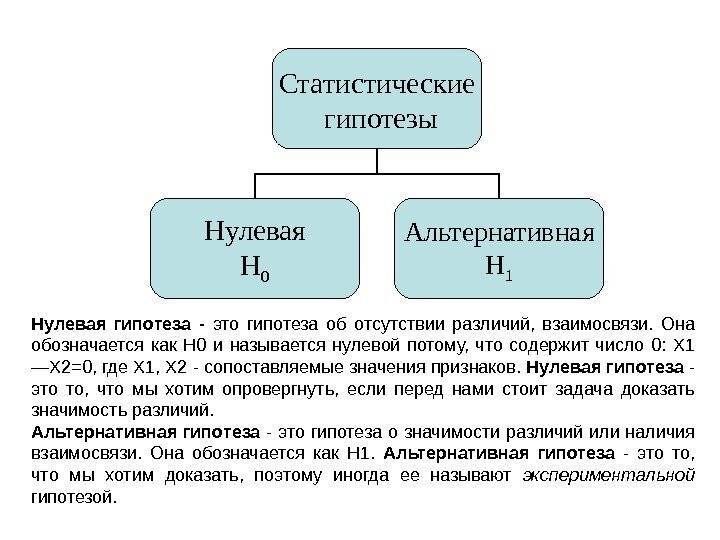
Основные определения

Нулевая гипотеза и альтернативная гипотеза типы гипотез , используемых в статистических тестах, которые являются формальными методами выработков заключений или принятия решений на основе данных. Эти гипотезы гипотеза о статистической модели от населения , которые основаны на выборке населения. Тесты являются ключевыми элементами статистического вывода , которые активно используются при интерпретации научных экспериментальных данных, чтобы отделить научные утверждения от статистического шума.

«Утверждение, проверяемое в тесте на статистическую значимость , называется нулевой гипотезой . Тест значимости предназначен для оценки силы свидетельств против нулевой гипотезы. Обычно нулевая гипотеза является утверждением« нет эффекта »или нет разницы’.” Часто обозначается как H .

Утверждение, которое проверяется против нулевой гипотезы, является альтернативной гипотезой . Символы включают H ₁ и H _a .

Тест статистической значимости: «В общих чертах процедура принятия решения выглядит следующим образом: возьмите случайную выборку из совокупности. Если данные выборки согласуются с нулевой гипотезой, то не отвергайте нулевую гипотезу; если данные выборки не согласуются с нулевую гипотезу, затем отклоните нулевую гипотезу и сделайте вывод, что альтернативная гипотеза верна “.

В следующих разделах к основным определениям добавляется контекст и нюансы.

Пример ошибок двух типов

Со сложными понятиями легче разобраться на примере.

Во время производства некоего лекарства от учёных требуется чрезвычайная осторожность, так как превышение дозы одного из компонентов провоцирует высокий уровень токсичности готового препарата, от которого пациенты, принимающие его, могут умереть. Однако на химическом уровне выявить передозировку невозможно.
Из-за этого перед тем как выпустить лекарство в продажу, небольшую его дозу проверяют на крысах или кроликах, вводя им препарат

Если большая часть испытуемых умирает, то лекарство в продажу не допускается, если подопытные живы, то лекарство разрешают продавать в аптеках.

Первый случай: на самом деле лекарство было не токсично, но во время эксперимента была допущена оплошность и препарат классифицировали как токсичный и не допустили в продажу. А=1.

Второй случай: в ходе другого эксперимента при проверке другой партии лекарства решено, что препарат не токсичен, и в продажу его допустили, хотя на самом деле препарат был ядовит. А=2.

Первый вариант повлечёт за собой крупные финансовые затраты поставщика-предпринимателя, так как придётся уничтожить всю партию лекарства и начинать с нуля.

Вторая ситуация спровоцирует смерть пациентов, купивших и употреблявших это лекарство.

Уровень значимости

Вероятность возникновения ошибки первого рода называется уровнем значимости (significance level). Уровень значимости обозначают буквой  $\alpha$. Поэтому ошибку первого рода иногда называют $\alpha$-ошибкой ($\alpha$-error). Обратное значение уровня значимости ($1-\alpha$) называется доверительной вероятностью или коэффициентом доверия (confidence coefficient).

Вероятность возникновения ошибки второго рода обозначают буквой $\beta$, поэтому сама ошибка называется $\beta$-ошибкой ($\beta$-error). Эта ошибка сама не используется в статистике, зато используется его обратная величина ($1-\beta$). Обратная величина $\beta$-ошибки называется мощностью критерия (power). Мощность критерия выражает вероятность правильного принятия альтернативной гипотезы.

В последнее время именно на мощность критерия больше всего обращают внимание. Потому что, исследователи и агентства не хотят тратить усилия и ресурсы на исследование области, если не будет достигнута разумная вероятность результата

Поэтому, чем больше мощность критерия, тем меньше вероятность возникновения ошибки второго рода.

Переменные потока и запасы

Все экономические переменные, которые имеют временное измерение, т.е. величины которых можно измерить по истечении времени называем переменными потока. А запас не имеет временное измерение.

Показатели вариации

Чтобы знать, насколько далеко значение совокупности простирается от центральной тенденции, вычисляют вариацию (на английском dispersion или variability, но не путайте с variation). Есть несколько показателей вариации. Это размах, межквартильный размах, среднее линейное отклонение, дисперсия и стандартное отклонение.

Типы выборки

Для расследования генеральной совокупности применяют два вида выборки. Случайную и неслучайную выборку. Простая, систематическая, стратифицированная и кластерная выборка являются случайными выборками. Стихийная, удобная и квотная выборка являются примером неслучайной выборки.

Скользящее среднее значение

Среди наиболее популярных технических индикаторов чаще всего, скользящее среднее значение используются для измерения направления текущего тренда. Самая простая формула скользящей средней, известна как Простое Скользящее Среднее значение.

Генеральная совокупность и выборка

Генеральной совокупностью называют всё исследуемое множество. На английском языке этот термин называется популяцией (population). Выборкой (на английском sample) называют некоторое случайно отобранное подмножество из генеральной совокупности.

Типы данных в статистике

Такие выражения, как минимум, максимум, медиана и процентиль имеют значение лишь для порядковых данных. Порядковые данные делятся на метрические и неметрические.

Что такое тренд?

Термины тренд и тенденция используются в различных целях. Люди часто говорят о тенденции относительно роста цен и падения курса какой-то валюты. Здесь мы раскроем статистическое значение этих терминов.

Ошибка репрезентативности

Стандартная ошибка (standard error) и ошибка репрезентативности часто употребляются, как взаимозаменяемые термины. Ошибка репрезентативности показывает, насколько результаты, полученные при выборочном наблюдении отличаются от результатов, полученных при исследовании генеральной совокупности.

Среднее значение, медиана и мода

Все чаще встречаем такие термины, как Бизнес-аналитика, Система поддержки принятия решений, Предсказательная аналитика. Но их уже достаточно распиарили и без нас. Поэтому остановимся на объяснении этих трех терминов: среднее значение, медиана и мода.

Типы статистических критериев

В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.

Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.

Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.

Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.

Критерии согласия

Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.

• Критерий Колмогорова-Смирнова
• Критерий хи-квадрат (Пирсона)
• Критерий омега-квадрат (фон Мизеса)

Критерии сдвига

Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.

• Критерий Стьюдента
• Критерий Уилкоксона-Манна-Уитни

Критерии нормальности

Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.

• Критерий Шапиро-Уилка
• Критерий асимметрии и эксцесса

Критерии однородности

Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.

Критерии симметричности

Критерии симметричности позволяют проверить симметричность распределения.

• Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
• Критерий знаков
• Коэффициент асимметрии

Критерии тренда, стационарности и случайности

Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.

«Доверительный» способ проверки

Существует наиболее действенный способ, с помощью которого нулевая статистическая гипотеза легко проверяется на практике. Он заключается в построении диапазона значений до 95% точности.

Для начала понадобится знать формулу расчёта доверительного интервала:
X – t*Sx ≤ c ≤ X + t*Sx,

где Х — данное изначально число на основе альтернативной гипотезы;
t — табличные величины (коэффициент Стьюдента);
Sx — стандартная средняя ошибка, которая рассчитывается как Sx = σ/√n, где в числителе стандартное отклонение, а в знаменателе – объём выборки.

Итак, предположим ситуацию. До ремонта конвейер в день выпускал 32.1 кг конечной продукции, а после ремонта, как утверждает предприниматель, коэффициент полезного действия вырос, и конвейер, по недельной проверке, начал выпускать 39.6 кг в среднем.

Нулевая гипотеза будет утверждать, что ремонт никак не повлиял на КПД конвейера. Альтернативная гипотеза скажет, что ремонт коренным образом изменил КПД конвейера, поэтому производительность его повысилась.

По таблице находим n=7, t = 2,447, откуда формула примет следующий вид:

39,6 – 2,447*4,2 ≤ с ≤ 39,6 + 2,447*4,2;

29,3 ≤ с ≤ 49,9.

Получается, что значение 32.1 входит в диапазон, а следовательно, значение, предложенное альтернативой — 39.6 — не принимается автоматически. Помните, что сначала проверяется на правильность нулевая гипотеза, а потом – противоположная.