NPV: формула расчета (пример)
Задача. Имеется три потенциальных проекта для инвестиций. Первоначальные инвестиции С в каждый из них составляют 400 условных единиц. Известна прибыль (Пn) , которую смогут генерировать проекты в ближайшие пять лет:
| Проект | Начальные инвестиции | Прибыль по годам | ||||
| П1 | П2 | П3 | П4 | П5 | ||
| Проект 1 | 400 | 80 | 105 | 120 | 135 | 150 |
| Проект 2 | 400 | 100 | 117 | 124 | 131 | 118 |
| Проект 3 | 400 | 100 | 125 | 90 | 130 | 145 |
Норма прибыли i составляет 13 %. Необходимо выбрать наиболее выгодный проект, используя формулу NPV.
Решение. Интересующая нас формула имеет следующий вид:
В этой формуле CFt обозначает чистый эффективный денежный поток на t-ом годичном интервале, i — ставка дисконтирования (в десятичном выражении), N – количество лет.
В представленной формуле главное разглядеть фактор (коэффициент) дисконтирования 1/(1 + i)t.
В нашем случае для t = 0 он будет равен 1, для t = 1: 1/(1+0,13)1 = 0,885 и т.д.
Рассчитаем значения NPV для каждого из трех проектов, используя табличное представление (оно более наглядно).
| Проект 1 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 80 | 0,885 | 70,80 |
| 2 | 105 | 0,783 | 82,22 |
| 3 | 120 | 0,693 | 83,16 |
| 4 | 135 | 0,613 | 82,76 |
| 5 | 150 | 0,543 | 81,45 |
| NPV = | 0,39 |
| Проект 2 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 117 | 0,783 | 91,61 |
| 3 | 124 | 0,693 | 85,93 |
| 4 | 131 | 0,613 | 80,30 |
| 5 | 118 | 0,543 | 64,07 |
| NPV = | 10,41 |
| Проект 3 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 125 | 0,783 | 97,88 |
| 3 | 90 | 0,693 | 62,37 |
| 4 | 130 | 0,613 | 79,69 |
| 5 | 145 | 0,543 | 78,74 |
| NPV = | 7,18 |
Наибольший NPV имеет проект 2. С точки зрения NPV, этот проект и является самым выгодным.
Разумеется, вместо таблиц мы бы могли использовать иное представление решения:
NPV1 = -400 * 1,000 + 80 * 0,885 + 105 * 0,783 + 120 * 0,693 + 135 * 0,613 + 150 * 0,543 = 0,39
NPV2 = -400 * 1,000 + 100 * 0,885 + 117 * 0,783 + 124 * 0,693 + 131 * 0,613 + 118 * 0,543 = 10,41
NPV3 = -400 * 1,000 + 100 * 0,885 + 125 * 0,783 + 90 * 0,693 + 130 * 0,613 + 145 * 0,543 = 7,18
Результат расчета NPV будет тот же.
На этом простом примере мы показали, как считать NPV, когда заранее известен объем первоначальных инвестиций и ожидаемые размеры прибыли на ближайшую перспективу.
На практике эти значения известны далеко не всегда, что существенно усложняет задачу выбора наиболее выгодного инвестиционного проекта.
Применение одного лишь метода NPV в таких ситуация может привести к неверным выводам: либо прибыль окажется невысока, либо ждать ее придется неоправданно долго.
Компенсировать недостатки NPV призваны другие расчетные показатели (уже упомянутый нами IRR, отражающий внутреннюю норму доходности, и некоторые другие).
Думается, после проработки сегодняшней статьи вы уже не будете задаваться вопросом при виде загадочной трехбуквицы NPV, что это такое и как рассчитать сей показатель.
Удачных инвестиций!
Что такое чистый дисконтированный доход?
Чистый дисконтированный доход (ЧДД или NPV) – показатель, характеризующий эффективность вложений в развитие конкретного направления, благодаря чему на протяжении срока его реализации можно наблюдать за величиной денежных потоков и анализировать ее.
Благодаря показателю NPV инвестор может сравнить проекты, куда предполагается вложить средства, определить их эффективность, принять окончательное решение о материальной поддержке.
Для чего используется ЧДД?
Главное предназначение NPV заключается в установлении прибыльности направления, в развитие которого будут вложены средства. Чтобы правильно определить эффективность проекта, следует провести его детальный анализ
При этом во внимание принимается не только срок вложений, длительность идеи и величина инвестиций, но также целесообразность данного вида деятельности. Другими словами, ЧДД показывает, нужно вкладывать деньги или нет. Благодаря расчетам временные рамки стираются, а результат приводится к текущему времени
Данный показатель очень удобен и эффективен, поскольку наглядное видение предполагаемой прибыли/убытка вложения денег позволит выбрать альтернативный вариант и станет страховкой инвестора от возможных потерь
Благодаря расчетам временные рамки стираются, а результат приводится к текущему времени. Данный показатель очень удобен и эффективен, поскольку наглядное видение предполагаемой прибыли/убытка вложения денег позволит выбрать альтернативный вариант и станет страховкой инвестора от возможных потерь.
Чтобы определить, насколько перспективным будет инвестируемый бизнес-проект, предстоит пройти несколько этапов:
- провести оценку движения денег по типу «вложение-результат»;
- рассчитать ставку – выяснить реальную стоимость активов;
- провести все потоки финансовых ресурсов через установленную ставку;
- сложить потоки, которые в совокупности и составят величину NPV.
Для чего нужен
NPV — один из показателей эффективности проекта, наряду с IRR, простым и дисконтированным сроком окупаемости. Он нужен, чтобы:
- понимать какой доход принесет проект, окупится ли он в принципе или он убыточен, когда он сможет окупиться и сколько денег принесет в конкретный момент времени;
- для сравнения инвестиционных проектов (если имеется ряд проектов, но денег на всех не хватает, то берутся проекты с наибольшей возможностью заработать, т.е. наибольшим NPV).
Показатели ЧДД
Выделяют три разных значения показателей ЧДД.
NPV ˃ 0 показывает, что инвестиции окажутся выгодными, но сравнение с другими направлениями вложений финансовых ресурсов должно быть проведено непременно до принятия окончательного решения. Тогда выбирается проект, показывающий наибольшую эффективность и прибыльность.
NPV ˂ 0 – инвестирование окажется нецелесообразным вследствие его убыточности.
NPV = 0 – при нулевом показателе ЧДД риск потери вложенных средств оказывается минимальным, но и сумма прибыли будет практически на нулевом уровне. По мере развития направление может начать постепенно окупаться, тем не менее инвесторы считают такие вложения нецелесообразными и чаще отказываются от них. Исключение имеет место, если преследуется не только финансовая цель, но также предполагается поддержка бизнес-идеи по другим параметрам (например, реализуется социально-значимый проект).
Достоинства и недостатки
К положительным качествам чистого дисконтированного дохода относятся:
- обозначение четких критериев, которыми руководствуются при принятии окончательного решения;
- стоимость денежных вложений учитывается в реальном времени (при помощи специальных формул);
- ЧДД показывает риск проекта.
К отрицательным качествам относятся:
- отсутствует гарантия определенного результата исхода событий. Другими словами, показатель не учитывает риски. Но это не такой уж большой недостаток, ведь именно ЧДД используется для выявления возможных рисков, связанных с инвестированием. Чем выше ставка дисконтирования, тем больший риск ожидает инвестора, и наоборот;
- не учитывает нематериальные ценности и имущество организации;
- ставка дисконтирования рассчитывается довольно сложно. Это может оказать влияние на итоговую величину дисконтированного дохода, исказить его результаты. Особенно часто такие ситуации возникают при реализации сложных проектов, сопряженных с большим количеством рисков.
Пример расчета по NPV
Чтобы лучше понять, как это работает, разберем примеры.
Инвестору предлагают два равно неизвестных варианта вложения денег. Условно обозначим эти проекты А и Б. При этом проект А обеспечивает резкий возврат средств, угасающий со временем. А проект Б увеличивает выгоды постепенно. Дисконт в обоих случаях составляет десять процентов. Схематически это выглядит примерно так:
А
| Год | Денежные средства |
| -20000 | |
| 1 | 10000 |
| 2 | 4000 |
| 3 | 3000 |
Б
| Год | Деньги |
| -10000 | |
| 1 | 1000 |
| 2 | 3000 |
| 3 | 5000 |
Рентабельность можно найти либо рассчитав все вручную, либо воспользовавшись программой Excel. В разделе экономических формул присутствует необходимая нам формула ЧПС.
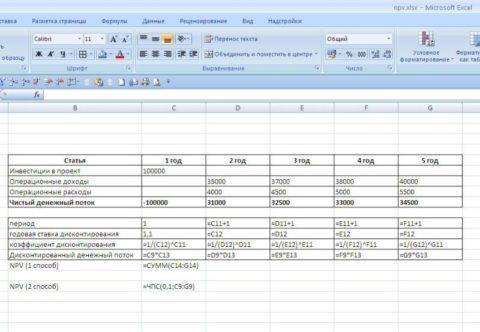
После всех вычислений получаем:
- Для А получаем, что значение отрицательно и равно минус 2400 рублей (-2400 руб.).
- Для Б – минус семьсот двадцать семь (-727 руб.).
Таким образом, для инвестиций оказался непригоден ни один из проектов. При том, что потери в проекте А больше.
Пример расчета NPV
Размер чистой приведенной стоимости инвестиций зависит от размера ставки дисконтирования, чем выше ставка дисконтирования, тем меньше NPV. Выбор ставки дисконтирования основывается на сравнении гипотетической доходности инвестиций в другие проекты или сравнение ее со стоимостью действующего капитала. Такое сравнение дает представление инвестору о барьере минимальной доходности от инвестиций в данном конкретном варианте вложений.

- стоимость действующего капитала в инвестируемом объекте обеспечивает доходность на уровне 16%;
- кредитные ставки банков равны 12 – 14%;
- банковские депозиты обеспечивают доходность 11 -13%;
- уровень доходности финансового рынка с минимальной степенью риска находится на уровне 15%.
Очевидно, что ставка дисконтирования должна быть несколько выше максимальной доходности всех возможных вариантов вложений средств, то есть выше или минимум равна 16%. При равной базовой ставке действующего капитала и норме дисконтирования речь может идти об инвестировании в расширение производства на существующей технологической и технической базе производства.
Вышеприведенная формула расчета NPV исходила из предположения, что инвестиции делаются одномоментно, в начале реализации проекта. В жизни часто такие вложения делаются в течение нескольких лет. В этом случае формула расчета приобретает следующий вид:
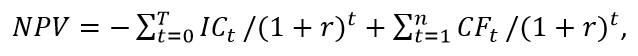
где:
- ICt – инвестиции в t-ом году;
- T – период вложений инвестиций.
В данной формуле инвестиционные потоки также приводятся по принятой ставке дисконтирования.
В инвестиционной практике довольно часто встречаются случаи, когда полученная прибыль реинвестируется на определенный период. Чаще всего такая ситуация возникает при недостатке финансирования проекта.
Тогда формула расчета изменяется следующим образом:
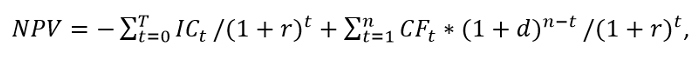
где:
d – процентная ставка реинвестирования капитала.
Для сравнительного анализа инвестиционных проектов соизмеряют их показатели NPV. Инвестиции с большим NPV, признаются предпочтительными.
Достоинством данного показателя является возможность определения чистой накопленной стоимости за весь жизненный цикл инвестиционного проекта, что позволяет сравнивать варианты инвестиций при различных жизненных циклах. Однако на основании этого показателя не всегда возможно ответить на вопрос, какой из вариантов более эффективен по доходности.

- 1 проект за 3 года (жизненный цикл) получит NPV в размере 200 млн. рублей.
- 2 проект в течение 5 лет (жизненный цикл) — 300 млн. рублей.
Их можно в данном случае сравнить по среднегодовому NPV:
- 1 вариант — 66,67 млн. рублей;
- 2 вариант — 60 млн. рублей.
1 вариант предпочтительнее, несмотря на больший размер NPV во 2 варианте. Поэтому, для более точной оценки прибегают к использованию среднегодовой нормы доходности инвестиций IRR, или сравниваемые варианты должны иметь одинаковый жизненный цикл, тогда вариант с большим NPV будет предпочтительнее.
Расчеты данного показателя, особенно для крупных инвестиций, сложны не только технически, но и методически. Первый недостаток легко преодолевается современными вычислительными устройствами, а второй может сказаться на точности проведенных расчетов и привести к неверным оценкам проекта. Поэтому с расчетом данного показателя всегда рассчитываются показатели дисконтированного срока окупаемости вложений DPP и внутренняя норма доходности IRR. Вкупе они дают высокую точность расчетов экономической эффективности любого инвестиционного проекта.
Чистый дисконтированный доход. Формула расчета
где: NPV – чистый дисконтированный доход инвестиционного проекта;
CFt(Cash Flow) – денежный поток в период времени t;
IC (Invest Capital) – инвестиционный капитал, представляет собой затраты инвестора в первоначальный временном периоде;
r – ставка дисконтирования (барьерная ставка).
Итак, для того чтобы рассчитать NPV необходимо спрогнозировать будущие денежные потоки по инвестиционному проекту, определить ставку дисконтирования и рассчитать итоговое значение приведенных к текущему моменту доходов.
Принятие инвестиционных решений на основе критерия NPV
Показатель NPV является одним из самых распространенных критериев оценки инвестиционных проектов. Рассмотрим в таблице, какие решения могут быть приняты при различном значении NPV.
| Оценка значения NPV | Принятие решений |
| NPV≤0 | Данный инвестиционный проект не обеспечивает покрытие будущих расходов или обеспечивает только безубыточность и его следует отклонить от дальнейшего рассмотрения |
| NPV>0 | Проект привлекателен для инвестирования и требует дальнейшего анализа |
| NPV1>NPV2 | Инвестиционный проект (1) более привлекателен по норме приведенного дохода, чем второй проект (2) |
Ставка в процентном выражении
Этот параметр в формуле расчёта чистой приведённой стоимости представлен размером капитала для инвестцелей. Иными словами, это цифра ставки %, интересной инвестфирме в целях привлечения сторонних финресурсов.
В стандартной ситуации организация может получить материальную помощь из трёх основных источников:

Те финресурсы, которые приходят из трёх разных источников, отличаются своей стоимостью. Проще всего разобраться с долговыми потоками. Они бывают представлены % по облигациям на долгосрок, ставками по кредитам. Оценить стоимость 2-ух оставшихся источников без соответствующих навыков очень проблематично. Опытными финансистами предложены универсальные схемы для изучения ситуации.
Стоимость принадлежащего бизнес-структуре капитала всегда будет представлена в виде средневзвешенной цифры % ставок из перечисленных трёх источников. Во многих англоязычных пособиях такой подход к работе обозначают аббревиатурой WACC, переводится она как «средневзвешенная стоимость капитала».
Что такое Чистая приведенная стоимость (NPV)?
Чистая приведенная стоимость (NPV) – это разница между текущей стоимостью денежных поступлений и текущей стоимостью оттока денежных средств за период времени. NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа прибыльности планируемых инвестиций или проектов.
Следующая формула используется для расчета NPV:
Если вы не знакомы с обозначением суммирования – вот более простой способ запомнить концепцию NPV:
NPVзнак равноТВЕСФ-ТВИСжчере:ТВЕСФзнак равноТодY’секпротивлуйоетчеехрестедсычелöже ТВИСзнак равноТодY’секпротивлуеоеянvéсектедр асекч \ begin {align} & \ textit {NPV} = \ text {TVECF} – \ text {TVIC} \\ & \ textbf {где:} \\ & \ text {TVECF} = \ text {Сегодняшняя сумма ожидаемых денежных средств потоки} \\ & \ text {TVIC} = \ text {Сегодняшняя стоимость вложенных денежных средств} \\ \ end {выровнено}Взаимодействие с другими людьмиЧПСзнак равноTVECF-TVICкуда:TVECFзнак равноСегодняшняя стоимость ожидаемых денежных потоковTVICзнак равноСегодняшняя стоимость вложенных денежных средствВзаимодействие с другими людьми
Положительная чистая приведенная стоимость указывает на то, что прогнозируемая прибыль, полученная от проекта или инвестиций – в текущих долларах – превышает ожидаемые затраты, также в настоящих долларах. Предполагается, что инвестиция с положительной NPV будет прибыльной, а инвестиция с отрицательной NPV приведет к чистому убытку. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительными значениями NPV.
Помимо самой формулы, чистую приведенную стоимость можно рассчитать с помощью таблиц, электронных таблиц или калькуляторов.
0:22
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание . В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция ПС() используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить ПС() рассчитать Приведенную стоимость и по методу простых процентов (см. файл примера ).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета Будущей стоимости (FV): FV = PV * (1+i*n) где PV – Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i – процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Преимущества и недостатки NPV
К положительным моментам методики NPV можно отнести:
- чёткие и простые правила для принятия решений относительно инвестиционной привлекательности проекта;
- применение ставки дисконтирования для корректировки суммы денежных потоков во времени;
- возможность учета премии за риск в составе ставки дисконтирования (для более рискованных проектов можно применить повышенную ставку дисконтирования).
К недостаткам NPV можно отнести следующие:
- трудность оценки для сложных инвестиционных проектов, которые включают в себя множество рисков особенно в долгосрочной перспективе (требуется корректировка ставки дисконтирования);
- сложность прогнозирования будущих денежных потоков, от точности которых зависит расчетная величина NPV;
- формула NPV не учитывает реинвестирование денежных потоков (доходов);
- NPV отражает только абсолютную величину прибыли. Для более корректного анализа необходимо также дополнительно производить расчёт и относительных показателей, например таких как рентабельность инвестиций, внутренняя норма доходности (IRR).
Формула [ править ]
Каждый приток / отток денежных средств дисконтируется до его приведенной стоимости (PV). Затем все суммируются. Следовательно, NPV – это сумма всех условий,
- рт(1+я)т{\ Displaystyle {\ гидроразрыва {R_ {t}} {(1 + я) ^ {t}}}}
куда
- т{\ displaystyle t} время денежного потока
- я{\ displaystyle i}ставка дисконтирования, то есть доход, который может быть получен в единицу времени на инвестиции с аналогичным риском.
- рт{\ displaystyle R_ {t}}– чистый денежный поток, т.е. денежный приток – денежный отток в момент времени t . В образовательных целях обычно помещается слева от суммы, чтобы подчеркнуть ее роль (минус) вложения.р{\displaystyle R_{0}}
Результат этой формулы умножается на годовой чистый приток денежных средств и уменьшается на первоначальные денежные затраты на текущую стоимость, но в случаях, когда денежные потоки не равны по сумме, для определения приведенной стоимости будет использоваться предыдущая формула. каждый денежный поток отдельно. Любой денежный поток в течение 12 месяцев не будет дисконтирован для целей NPV, тем не менее, обычные первоначальные инвестиции в течение первого года R суммируются с отрицательным денежным потоком.
Учитывая пары (период, денежный поток) ( , ), где – общее количество периодов, чистая приведенная стоимость определяется по формуле:
t{\displaystyle t}Rt{\displaystyle R_{t}}N{\displaystyle N}NPV{\displaystyle \mathrm {NPV} }
- NPV(i,N)=∑t=NRt(1+i)t{\displaystyle \mathrm {NPV} (i,N)=\sum _{t=0}^{N}{\frac {R_{t}}{(1+i)^{t}}}}
Для постоянного денежного потока чистая приведенная стоимость представляет собой конечный геометрический ряд и определяется по формуле:
R{\displaystyle R}NPV{\displaystyle \mathrm {NPV} }
- NPV(i,N,R)=R(1−(11+i)N+11−(11+i)),i≠{\displaystyle \mathrm {NPV} (i,N,R)=R\left({\frac {1-\left({\frac {1}{1+i}}\right)^{N+1}}{1-\left({\frac {1}{1+i}}\right)}}\right),\quad i\neq 0}
Включение термина важно в приведенных выше формулах. Типичный капитальный проект включает в себя большой отрицательный денежный поток (начальные инвестиции) с положительными будущими денежными потоками (возврат инвестиций)
Ключевой оценкой является то, является ли NPV для данной ставки дисконтирования положительной (прибыльной) или отрицательной (убыточной). IRR – это ставка дисконтирования, для которой NPV ровно 0.
R{\displaystyle R_{0}}R{\displaystyle R_{0}}
Пример расчета
Компания рассматривает возможность реализации двух проектов, требующих одинаковых первоначальных инвестиций в размере 5 млн. у.е. При этом, оба обладают одинаковым риском неопределенности денежных потоков, и стоимостью привлечения капитала в размере 11,5%. Разница заключается в том, что по Проекту А основные поступление денежных потоков ожидаются раньше, чем по Проекту Б. Детальная информация об ожидаемых денежных потоках представлена в таблице.
Подставим имеющиеся данные в приведенную выше формулу рассчитаем значение чистой приведенной стоимости.
Дисконтированные денежные потоки по двум проектам представлены на рисунке ниже.
Если проекты являются независимыми, компания должна принять каждый из них. Если реализация одного проекта исключает возможность реализации другого, принять следует Проект А, поскольку он характеризуется более высоким NPV.
Расчет NPV в Excel
Рассчитать значение чистой приведенной стоимости можно также при помощи функции «ЧПС» в Excel, как показано на рисунке ниже.
- Выберите ячейку вывода H6.
- Нажмите кнопку fx, выберите категорию «Финансовые», а затем функцию «ЧПС» из списка.
- В поле «Ставка» выберите ячейку C1.
- В поле «Значение1», выберите диапазон данных C6:G6, оставьте пустым поле «Значение2» и нажмите кнопку OK.
Поскольку мы не учли первоначальные инвестиции, выберите ячейку вывода H6 и прибавьте ячейку B6 в строке формул.
Преимущества и недостатки метода чистой приведенной стоимости
Преимуществом метода NPV для при оценке проектов является использование методики дисконтированных денежных потоков, что позволяет оценить величину дополнительно создаваемой стоимости. Тем не менее, для этого метода характерны ряд недостатков и ограничений, которые необходимо учитывать при принятии решений.
Чувствительность к ставке дисконтирования. Одним из основных предположений является то, что все денежные потоки проекта реинвестируются по ставке дисконтирования. На самом деле, уровень процентных ставок постоянно меняется в следствие изменений экономических условий и ожиданий относительно уровня инфляции. При этом эти изменения могут носить значительный характер, особенно в долгосрочной перспективе. Таким образом, фактическое значение чистой приведенной стоимости может существенно отличаться от ее первоначальной оценки.
Денежные потоки после планируемого срока реализации. Некоторые проекты могут генерировать после запланированного срока реализации проекта. Эти денежные потоки могут обеспечить дополнительную стоимость к первоначальной оценке, но они игнорируются данным методом.
Управленческие опционы. В течение жизненного цикла проекта менеджмент компании может предпринять какие-либо действия, влияющие на сроки его реализации и масштаб в ответ на изменения рыночных условий. Эти действия могут изменить как время возникновения, так и величину ожидаемых денежных потоков, что приведет к изменению оценки чистой приведенной стоимости
Традиционный анализ дисконтированных денежных потоков не принимает во внимание такие изменения.
- ← Дисконтированный срок окупаемости
- Индекс рентабельности, PI →


































