Как посчитать процент от числа при расчёте налогов, кредитов и вкладов

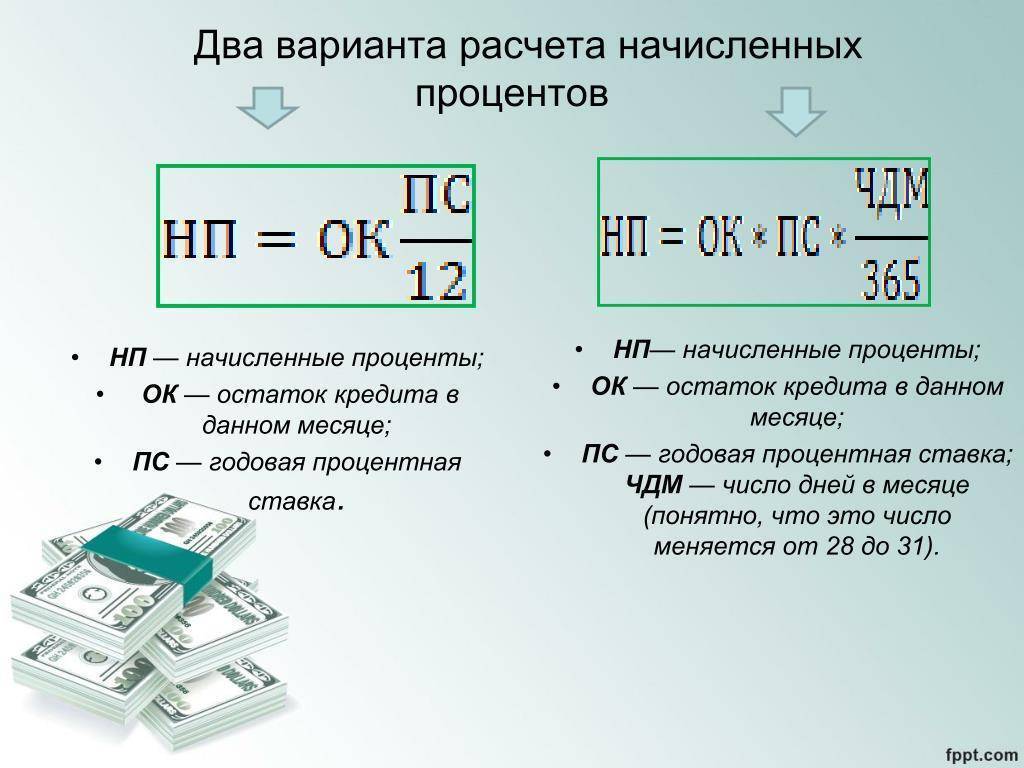
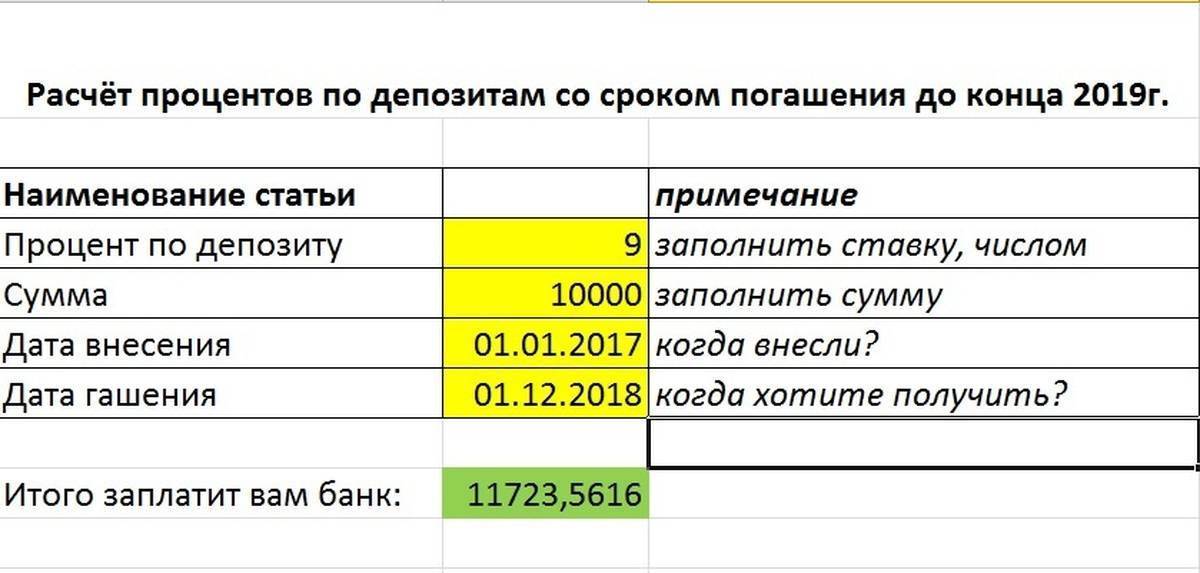
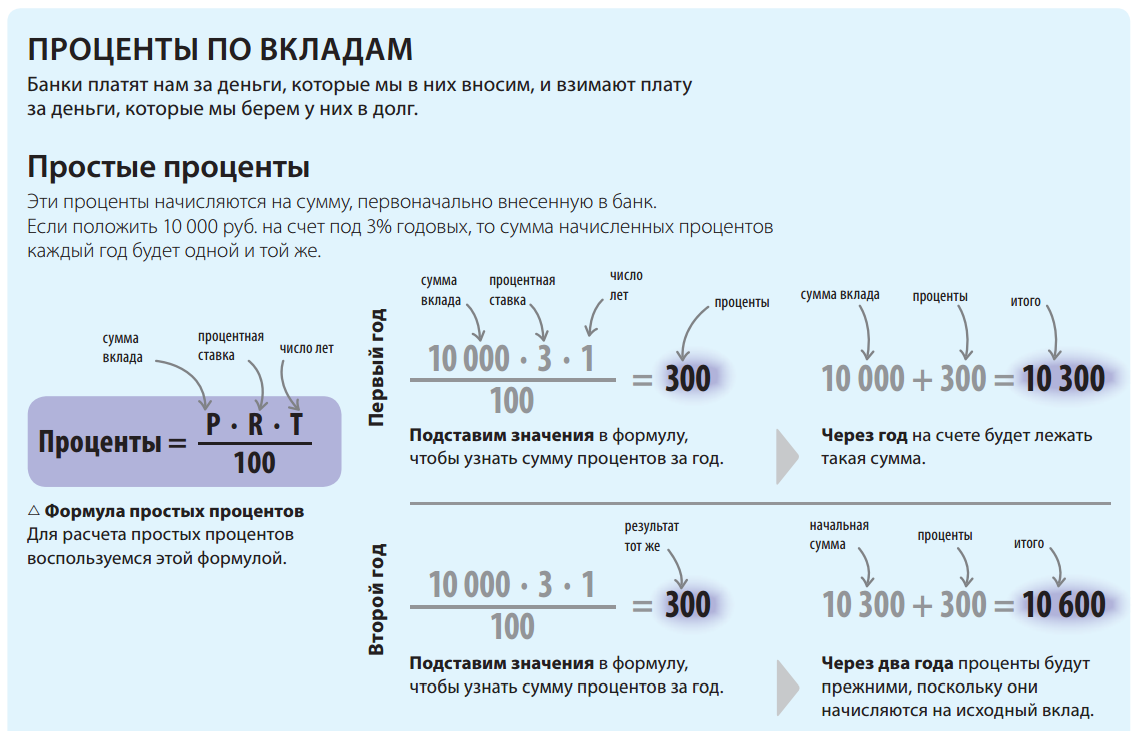
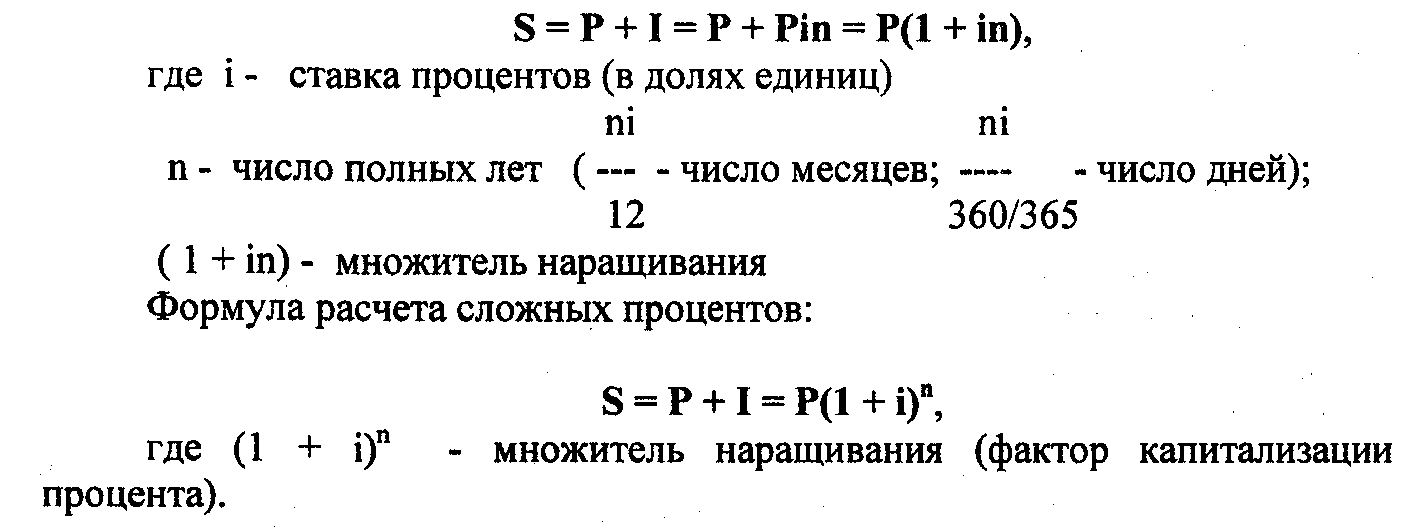Виды ежемесячных выплат по кредитам

Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.

Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.

В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.

Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.

Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.

Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю

Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.

Расчет вкладов, позволяющих делать пополнения и снятия

Вы можете задать параметры пополнений и снятий, а также сумму неснижаемого остатка по вкладу. Расчет будет произведен с учетом пополнения и снятий и вы получите результирующую сумму вклада.
Вклад с пополнениями позволяет накапливать средства, например на первоначальный взнос в ипотеку. Накопление средств на ипотеку посредством депозита достаточно распространенный способ купить квартиру. К нему прибегают многие россияне.
Калькулятор вкладов помогает понять, сколько денег у вас будет в конце накопления и по скольку нужно пополнять, чтобы хватило на первоначальный взнос. Естественно депозит нужно открывать как можно максимальный процент и с капитализацией. Такие вложения являются самыми выгодными и безопасными. Другими способами приумножить ваши деньги — является игра на бирже или вложение средств в себя. Но эти затраты не гарантируют стопроцентную окупаемость. Депозит же отличает стабильность, вы всегда знаете, что ваши деньги вернутся к вам благодаря системе страхования вкладов от государства. Но это касается вкладов менее 1400 тыс.

Налог на доход от вклада

С 2021 г. появился налог на доходы от вклада превышающих 1 млн рублей. Также есть два условия, когда есть обязательный налог:

1. Если ставка по вкладу выше, чем ключевая на 5 базисных пункта;
2. На валютные вклады свыше 9% годовых;

Если выполняется одно из двух условий, то берётся налог только со сверхдохода. Ставка налога составляет 30% для резидентов РФ и 35% для нерезидентов.

Например, если ключевая ставка ЦБ составляет 8%, а банковский депозит 15%, то превышение составляет 2% (8%+5%=13% – максимально возможная ставка без налога). На доход с 2% будет браться налог.

Примечание

Текущая ключевая ставка ЦБ 7,50% (изменение от 22 октября 2021 года).

Как рассчитать сумму процентов кредита по ежемесячному аннуитетному платежу

Если понятие дифференцированный кредит узнаваемо всеми, то термин «аннуитетный» не так распространён. Такой займ подразумевает погашение долга равными частями. То есть высчитать сколько средств следует вносить на счёт каждый месяц заново не придётся. На протяжении всего займового периода платежи не меняются. Однако сама ставка и процент рассчитываются немного другим способом, более сложным. Опять же, для упрощения задачи рациональнее посчитать через калькулятор процентов по кредиту.

Чтобы рассчитать сумму ежемесячного платежа, не прибегая к помощи специального калькулятора процентов по кредиту, воспользуйтесь такой формулой:

Теперь расшифруем необходимые для высчитывания значения (кстати, калькулятор здесь в любом случае понадобится, иначе рискуете неправильно рассчитать сумму):

• ПСЗ – первичная сумма займа.
• ГПС – годовой процентный размер.
• КП – запланированное количество платежей по займу.

По этой формуле придётся считать платёж с возведением в степень и многоуровневым делением, поэтому проще использовать калькулятор кредита онлайн с процентами.

Как рассчитать процент от суммы

Очень часто приходится сталкиваться с несколькими искомыми числами или их суммой. Вопрос о том, как расчитывать проценты от суммы, решается так же просто, как и в случае использования одного начального числа. Единственное, что нужно учесть в этом случае, так это обычное представление суммы в виде единого значения.

Например, у нас имеется два числа, a и b, и начальным показателем выступает число d. В данном случае пропорция будет выглядеть следующим образом:

Заметьте, сумму (a + b) все равно можно представить в виде единого числа. Пускай это будет z. В случае, когда мы задаем формулу a + b = z, пропорция приобретает совершенно стандартный вид:

Как видим, ничего сложного в этом нет.

Есть и другой вариант, когда сумма (a + b) = 100%, а d = x.

Тут решение выглядит так:

(d x 100)/(a + b) или (d/(a + b)) + 100/(a + b).

Как уже понятно, здесь используется принцип общего знаменателя для дробей.

Если сложить a и b, сумма которых равна z, то пропорция опять возвращается к стандартному виду:

То же применяется и в обратном порядке.

Простые проценты (срочный вклад)

Чаще всего банковские вклады относятся к виду “срочных”. Данный тип вклада самый популярный среди населения за счёт самого большого процента из всей линейки банковских предложений.

Однако за такую щедрость от банка клиентам необходимо принять следующие условия:

• Отсутствие возможности снять средства частично на весь срок действия договора;
• Без пополнения;
• Проценты начисляются один раз в конце срока (без капитализации);

Пример 1. Срок 1 год, ставка 8% годовых

Вклад имеет ставку 8% годовых, без пополнения и открывается сроком на 1 год. В этом случае проценты по вкладу можно рассчитать на любом калькуляторе, умножив стартовую сумму на коэффициент 0,08 (8%).

Формула расчёта процентов по вкладу на 1 год:

Например, если сумма была 200 тыс. рублей, то прибыль за год составит 16 тыс. рублей, а итоговая сумма будет 216 тыс. рублей.

Естественно, в зависимости от ставки депозита умножать сумму необходимо на различные суммы.

Пример 2. Срок полгода, ставка 9% годовых

Немного более сложный пример. Теперь срок полгода со ставкой 9% годовых. Скорее всего, в договоре на банковский вклад будет обозначено число 181 день, а это чуть меньше, чем полгода. Поэтому необходимо будет рассчитывать процент с учётом этого нюанса.

Формула расчёта процентов на полгода:

Если наша сумма была 95 тыс. рублей, то за 181 день прибыль составит 4239,86 рублей.

В этой формуле используется коэффициент 181/365, поскольку наш депозит будет лежать 181 дней из 365 дней. Аналогичным образом можно рассчитать проценты по вкладу на любой срок с точностью до дня.

Пример 3. Срок 145 дней, ставка 8,7% годовых

Многие банки разрешают открывать вклад не только на точные сроки по месяцам, но и по дням. Например, так можно сделать в Сбербанке и Финам Банке. Это удобно для клиентов.

В нашем примере мы открываем вклад на 145 дней под ставку 8,7% годовых.

Формула для расчёта процентов по вкладу по дням:

Вместо 145 дней и ставки 8,7% необходимо подставить ваши данные.

Самостоятельный подсчет при аннуитетных платежах

Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:

1. Процентная ставка — 18%.
2. Период кредитования — 24 месяца.
3. Сумма кредита — 500000 рублей.

Классическая формула для расчета аннуитетного платежа выглядит так:

Разовый аннуитетный платеж = Сумма кредита * Ка

где Ка — это коэффициент аннуитета.

Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)

где ЕПС — ежемесячная процентная ставка.

Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.

Итоговый расчет примет вид:

500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.

Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.

Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:

24 962,05 * 24 = 599 089,24 рублей.

Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.

Расчет сложных процентов по вкладу

Если вам необходимо рассчитать сложные проценты по вкладу — это будет несколько сложнее. Для этого используется следующая формула.

Формула сложных процентов по вкладу:

S_п = S_в*(1+%)n-S_в

где:

• S_п — сумма процентов по вкладу;
• S_в — сумма вклада;
• % — процентная ставка в период капитализации в виде десятичной дроби. % = p*N_д/N_г (p — процентная ставка по вкладу в виде десятичной дроби, N_д — период капитализации в днях (месяцах), N_г — количество дней (месяцев) в году);
• n — число периодов капитализации.

Как вы видите, для расчета нам понадобится функция возведения в степень. Она есть на стандартном калькуляторе для Windows. Чтобы ее увидеть — измените через меню вид калькулятора на «инженерный». Xy — это и есть функция возведения в степень. Например, чтобы возвести 1,01 в 12 степень, нажмите на калькуляторе последовательно: 1,01 -> Xy -> 12 -> =.

Рассмотрим, как рассчитать сложный процент по вкладу по формуле сложных процентов на примере.

Расчет годовых процентов по кредиту

Все намного сложнее с кредитами. Здесь два способа начисления процентов:

1. дифференцированный;
2. аннуитетный.

Если с дифференцированным методом можно разобраться, то по аннуитету научиться вычислять суммы процентов за любой период не получиться. Только с помощью кредитного калькулятора. Этот способ родился в недрах ипотечного кредитования.

Однако сегодня не только ипотека, но и обычные займы погашаются по этому алгоритму, что затрудняет кредиторам возможность самостоятельно вести расчеты и, главное, делает невыгодным досрочное погашение кредита. Пример показывает Сбербанк, где все кредитные линии предусматривают аннуитетный способ погашения займов.

Для тех, кто попытается разобраться в этой сложной системе, советуем посмотреть статью «Аннуитетные и дифференцированные платежи» на нашем сайте. Остальным напомним порядок уплаты задолженности по кредиту дифференцированным способом.

Для конкретного расчета возьмем следующие цифры:

• сумма займа 125 000 руб.;
• срок действия договора 12 месяцев;
• ставка — 10 процентов годовых.

За первый месяц кредитору нужно выплатить банку тело кредита в сумме 124 964 руб. (125 000 / 36). За пользование ссудой необходимо платить проценты (расчет ведется по формуле простых процентов по вкладам, поэтому отдельно приводить ее нет необходимости). Их сумма составит 1061 руб. 64 коп. ((125 000 х 10,0 х 31 / 365) / 100) (арифметическое действие 31 / 365 можно заменить на 1 / 12, где дни переведены в месяцы).

После уплаты половины кредита, сумма процентов составит 530 руб. 82 коп. ((62 500 х 10,0 х 31 / 365) / 100). Это ровно в два раза меньше.

Как работает сложный процент?

Сложный процент подразумевает использование начальной суммы и дохода, полученного во время предыдущих периодов. Таким примером может являться вклад в банке, в условиях которого указана капитализация полученной прибыли. Сумма процентов по вкладу, начисленная за первый месяц, добавляется к основному счёту, и во второй год процентная ставка применяется уже к увеличенной сумме, что обеспечивает рост итоговой прибыли.

Формула сложного процента

Расчёт будущей прибыли при использовании сложного процента производится по формуле:

, где:

– сумма, которую вы получите в конце периода;

– сумма первоначальных инвестиций, т.е. то, что вы вкладываете;

– годовая ставка;

– количество периодов начисления ставки (ежемесячно, ежеквартально, ежегодно и т.д.);

– общий срок вклада в годах.

Пример сложных процентов

Как мы выяснили выше, при использовании сложных процентов, прибыль по вкладу постоянно увеличивается. Сейчас посмотрим на примере, как это происходит.

Предположим, что у нас открыт вклад на сумму в 1000$ на 1 год со ставкой 5%. В этом случае, доход в конце года будет: 1000$ + 1000$ * (5 / 100) = 1050$. То есть мы просто посчитали простой процент для вклада на один год. Затем мы решили, что хотим снова открыть вклад ещё на 1 год. Тогда мы возьмём полученные ранее 1050$ и снова добавим их на вклад под 5% годовых. Тогда получится: 1050$ + 1050$ * (5 / 100) = 1102.5$.

Как видите, в первый год мы получили 1050$, а на второй год 1102$. Это и есть пример работы сложного процента, т.е. когда результат первого года (те самые 1050$), мы использовали для процента второго года и тем самым получили 1102$.

Если бы во второй год мы использовали простой процент, то мы брали не результат прошлого года (1050$), а взяли снова 1000$. И получилось бы:

• 1 год: 1050$
• 2 год: 1050$
• 3 год: 1050$
• 4 год: 1050$
• 5 год: 1050$

Спустя 5 лет, на вашем депозите будет 5250$. А вот как меняется ваш депозит, если используется сложный процент:

• 1 год: 1050$
• 2 год: 1102$
• 3 год: 1157$
• 4 год: 1215$
• 5 год: 1276$

То есть, спустя 5 лет, на вашем депозите будет 5800$. Как вы видите, разница существенна и именно в этом магия сложного процента. Чем дольше вы вкладываете деньги, используя прибыль, накопленную за предыдущие года – тем выше будет доход в конце.

Разница между простым и сложным процентами

Основная разница между двумя типами процента в том, на что именно начисляется процент. Когда используется простой, то за основу вычислений всегда берётся первоначальная сумма

Неважно, делаете вы расчёт для первого года или третьего – сумма всегда одна. Для сложного же процента – основа вычислений, это результат предыдущих вычислений

То есть то, что вы рассчитывали для прошлого года, берётся за основу расчётов для текущего года. Кратко: простой процент – основа всегда одинакова, сложный процент – основа всегда разная.

Отличия между сложными и простыми процентами

Простой процент	Сложный процент
Доход начисляется один раз – в конце срока	Доход начисляется каждый год
При расчёте учитывается только начальная сумма	При расчёте учитывается начальная сумма плюс доход каждого года
Прибыль каждый год будет одинаковая.	Прибыль каждый год будет увеличиваться, то есть она всегда разная.

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Годовой процент кредита: расчет по формуле

Сегодня спрос на кредиты огромен, но популярность того или иного кредитного продукта зависит от годовой процентной ставки. В свою очередь, от процентной ставки зависит и сумма ежемесячного платежа.

Рассматривая вопрос о начислении процентов по кредиту, необходимо ознакомиться с основными определениями и особенностями кредитования в российских банковских учреждениях.

Годовая процентная ставка — это денежная сумма, которую заёмщик обязуется платить в конце года. Однако расчет процентов, как правило, производится на месяц или на день, если речь идет о краткосрочных кредитах.

Какой бы привлекательной не выглядела процентная ставка по кредиту, стоит понимать, что кредиты никогда не выдаются на бесплатной основе

Неважно, какой вид кредита берется: ипотека, потребительский или авто-кредит, все равно банку будет выплачена сумма больше, чем взяли. Чтобы рассчитать сумму ежемесячных выплат, необходимо разделить годовую ставку на 12. В некоторых случаях, кредитодатель устанавливает ежедневную процентную ставку

Перед подписанием кредитного договора рекомендуется тщательно проанализировать свое финансовое положение, а также сделать прогноз на будущее. Сегодня средняя ставка в российских банках составляет примерно 14%, поэтому переплата по кредиту и ежемесячные выплаты могут быть достаточно большими. Если заемщик будет не в состоянии погасить долг, это приведет к наложению штрафных санкций, судебным процессам и потери имущества.

Особую категорию займов составляют кредитные карты — проценты по кредиту не начисляются, если потраченные денежные средства своевременно вернуть банку.

Также стоит знать, что процентные ставки могут быть различными по своему состоянию:

• постоянная — ставка не меняется и устанавливается на весь срок погашение кредита;
• плавающая зависит от многих параметров, например от курса валют, инфляции, ставки рефинансирования и пр.;
• многоуровневая — основным критерием ставки является сумма оставшейся задолженности.

Ознакомившись с основными понятиями, можно переходить к расчету процентной ставки по кредиту. Для этого необходимо:

1. Узнать баланс на момент расчетов и величину долга. Например, баланс равен 3000 руб.
2. Узнать стоимость всех элементов кредита, взяв выписку по кредитному счету: 30 руб.
   Воспользовавшись формулой, разделить 30 на 3000, получится 0,01.
3. Полученное значение умножаем на 100. В результате получается ставка, регулирующая месячные выплаты: 0,01 х 100 = 1%.

Для расчета годовой ставки нужно 1% умножить на 12 месяцев: 1 х 12 = 12% годовых.
Ипотечные кредиты рассчитываются намного сложнее, т.к. включают множество переменных. Для корректного расчета, суммы кредита и процентной ставки будет недостаточно. Лучше использовать калькулятор, который поможет рассчитать примерную ставку и размер ежемесячных выплат по ипотеке.

Математическое объяснение

С точки зрения математики и ее основ решение задачи о том, как рассчитать процент от суммы, сводится только к применению простейших правил раскрытия скобок при умножении суммы на единое число и поиска общего знаменателя, который, в общем-то, им и является. Другими словами, представить в формульном выражении это можно так:

a x (b + c) = ab + ac ,

где ab и ac — произведения слагаемых в скобках (b и c) на число (коэффициент) перед скобками a.

Собственно, в пропорции действует тот же метод. Допустим, у нас есть некое число z, представляющее собой 100%, и сумма чисел a и b. Процент, который нужно вычислить, обозначим неизвестным числом y. В таком варианте пропорция принимает вид:

Отсюда простое решение:

((a + b) x 100%)/z = ((a x 100%) + (b x 100%))/z

В скобки действия взяты для того, чтобы подчеркнуть, что операции умножения выполняется в первую очередь, а сложение произведений — во вторую. Такое же действие производится, если изначально сумма чисел составляет 100%.

Аннуитетный или дифференцированный: наименьшие выплаты процентов по кредиту

Итак, рассчитывать проценты и размер ставок можно двумя методами: при помощи специального кредитного калькулятора или посчитать самостоятельно по формуле. Но один вопрос всё же остаётся нераскрытым: какая выплата окажется более выгодной – дифференцированная или аннуитетная?

По-сути, достоинства и недостатки подсчётов есть у обеих систем. Выбирать следует самостоятельно, отталкиваясь от реальных возможностей выплаты. Рекомендуется предварительно произвести расчёт процентов по кредиту с помощью калькулятора онлайн или считать самостоятельно, используя приведённые формулы. На основе полученной вычисленной информации подбирать подходящий способ выплаты займа.

Формула, как посчитать простые проценты от суммы вклада

Для здоровой экономики инфляция – обычный и даже необходимый процесс, который полезен и для производителей, и для потребителей. Однако если хранить деньги «под подушкой», их покупательная способность снизится. Избежать потерь можно, открыв вклад в банке. Финансовое учреждение получает средства, необходимые для его деятельности, а клиентам начисляет проценты за пользование их накоплениями. Предлагаем разобраться, в чем плюсы и минусы этого сотрудничества и как снять деньги с депозита, если возникла такая необходимость.

Чтобы понять, как посчитать годовой процент от суммы вклада с простым начислением, взгляните на эту формулу:

S = (P x I x t / K) / 100, где:

S — сумма начисленных процентов;

Р — вносимая сумма;

I — годовая процентная ставка по вкладу;

t — период, за который будут насчитаны проценты, в днях;

K — количество дней в году (год бывает и високосный).

Посчитать легко: клиент решил открыть депозит простого типа, внес 100 тысяч рублей на 1 год под 11,5 % годовых. Посчитаем и узнаем, что при окончании срока вклада человек получит доход в размере (100 000 х 11,5 х 365/365)/100 = 11 500 рублей.

Экономические вычисления

Узнать фактический удельный вес различных чисел, ориентируясь на одно, итоговое значение. Подобное используется в статистике или экономике. Формула аналогичная, единственная разница – знаменатель всегда одинаковый. Для Excel это обозначается «$».

Формула:

A2/$B$2

Пример расчета:

Известно, сколько молока надоено всего и по сколько дала каждая корова. Нужно выяснить фактический удельный вес (размер вклада) каждой коровы.

Если известны лишь индивидуальные результаты, без одного, конечного значения, вычислить его поможет несложная формула: =СУММ(номер ячейки первый-последний). Аналогичным образом несложно проверить произведенный расчет значений удельного веса.

Видна формула, прописанная наверху.

Рассчитывается удельный вес.

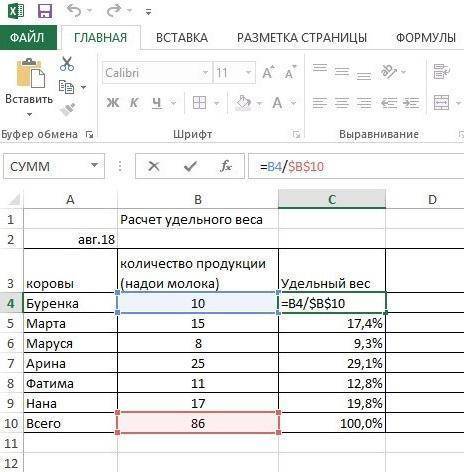
Получается, все величины надоев автоматически делятся на одну, «86» конечную величину.

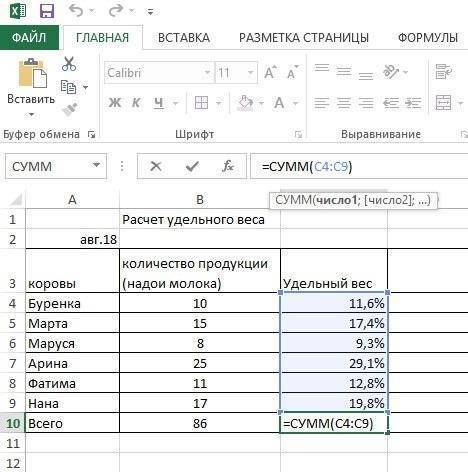
В конце столбика «удельный вес» после сложения вышло 100%, значит, расчет верен.

Темпы роста или же прироста показателя рассчитываются иначе:

1. Темп роста = прошедший период/текущий (в ячейке, где прописывается данная формула, устанавливается % формат).
2. Темп прироста = (текущий период – предыдущий)/предыдущий

Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то сумма вклада с процентами вычисляется по формуле сложных процентов.

S = K * ( 1 + P*d/D/100 ) N

Где: S — сумма депозита с процентами, К — сумма депозита (капитал), P — годовая процентная ставка, N — число периодов начисления процентов.

При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход):

Sp = S — K = K * ( 1 + P*d/D/100 ) N — K

Sp = K * (( 1 + P*d/D/100 ) N — 1)

Пример 1. Принят депозит в сумме 100 тыс. рублей сроком на 90 дней по ставке 20 процентов годовых с начислением процентов каждые 30 дней.

S = 100000 * (1 + 20*30/365/100) 3 = 105 013.02 Sp = 100000 * ((1 + 20*30/365/100) N — 1) = 5 013.02

Пример 2. Проверим формулу начисления сложных процентов для случая из предыдущего примера.

Разобьем срок депозита на 3 периода и рассчитаем начисление процентов для каждого периода, использую формулу простых процентов.

S₁ = 100000 + 100000*20*30/365/100 = 101643.84 Sp₁ = 100000 * 20*30/365/100 = 1643.84

S₂ = 101643.84 + 101643.84*20*30/365/100 = 103314.70 Sp₂ = 101643.84 * 20*30/365/100 = 1670.86

S₃ = 103314.70 + 103314.70*20*30/365/100 = 105013.02 Sp₃ = 103314.70 * 20*30/365/100 = 1698.32

Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)

Таким образом, формула вычисления сложных процентов верна.

Как рассчитать разные платежи по кредиту

Существует две схемы, по которым рассчитываются займы в банке — аннуитетная и дифференцированная. Первый вариант предусматривает более дорогие кредиты, поскольку процент начисляется на весь объем ссуды. Второй вариант подразумевает процентную ставку по кредиту с учетом предыдущих выплат, поэтому такой заем будет немного дешевле. Можно пересчитать ссуду по двум формулам — аннуитетной и дифференцированной и убедиться в этом лично.

Оформить дифференцированный заем намного сложнее, поскольку банки теряют на этом свой заработок. В том случае, когда это удается, нужно внимательно прочитать договор и убедиться, что отсутствуют дополнительные платежи, которыми кредитор захочет компенсировать потерянные деньги.

Изучая кредитную информацию, заемщикам необходимо внимательно ознакомиться с требованиями и условиями банков. Во время подписания бумаг стоит перечитать все пункты и задать интересующие вопросы по полученному договору. Также стоит перепроверить ежемесячные платежи, размер которых вычисляется по формулам, указанным выше.

Аннуитетные платежи

Аннуитетные платежи подразумевают наличие выплат равными частями на протяжении всего срока кредитования. Обязательный взнос, который необходимо перечислять на счет кредитора, состоит из двух частей — тела и процентов от суммы кредита. Такой способ расчета в интересах банка, поэтому аннуитетные займы предоставляются в большинстве кредитных организаций и имеют оптимальную годовую ставку.

Правильно рассчитать взнос по аннуитетной схеме легче, поскольку весь долг делится на равные части. Определить объемы выплат и сравнить результат с графиком, выданным банком, должен каждый заемщик. Это позволит избежать таких ситуаций, когда клиент погасил весь заем, а некоторая задолженность осталась

Важно мониторить свой счет, платеж сохранять в личном кабинете или распечатывать квитанцию

Дифференцированные платежи

Дифференцированная система кредитования подразумевает изменение ежемесячных выплат в зависимости от остатка долга. Тело займа разделяется на равные части исходя из количества платежей, а процент высчитывается от объема средств, которые остались для погашения. Таким образом, с каждым месяцем кредитные выплаты, которые необходимо осуществить заемщику, уменьшаются.

Кредиторы редко используют дифференцированную систему, поскольку она снижает стоимость займа. Кроме того, при дифференцированном расчете проще погасить долг досрочно, что значит — меньше будет заработок у банковских компаний. Финансовым структурам выгоднее получать стабильный доход в месяц, чем предоставлять недорогое кредитование.

Для подсчета выплат в рамках дифференцированного кредитования лучше использовать таблицу, в которую будет занесена определенная сумма долга каждый месяц на весь срок займа. Какой бы репутацией ни славился банк, необходимо самостоятельно перепроверить график платежей и удостовериться, что нет никаких ошибок.